题目内容
【题目】坐标系与参数方程
在平面直角坐标系中,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,已知直线
轴正半轴为极轴建立极坐标系,已知直线![]() 上两点
上两点![]() 的极坐标分别为
的极坐标分别为![]() .
.
(1)设![]() 为线段
为线段![]() 上的动点,求线段
上的动点,求线段![]() 取得最小值时,点
取得最小值时,点![]() 的直角坐标;
的直角坐标;
(2)求以为![]() 为直径的圆
为直径的圆![]() 的参数方程,并求在(1)条件下直线
的参数方程,并求在(1)条件下直线![]() 与圆
与圆![]() 相交所得的弦长.
相交所得的弦长.
【答案】(1)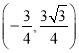 (2)3
(2)3
【解析】
试题分析:(1)先根据![]() 将
将![]() 的极坐标化为直角坐标
的极坐标化为直角坐标![]() ,再根据两点式求出线段
,再根据两点式求出线段![]() 所在直线方程
所在直线方程![]() ,由图可知当线段
,由图可知当线段![]() 时,线段
时,线段![]() 获得最小值,此时由直线方程联立方程组可解交点坐标
获得最小值,此时由直线方程联立方程组可解交点坐标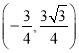 (2)先求出以
(2)先求出以![]() 为直径的圆
为直径的圆![]() 直角坐标方程
直角坐标方程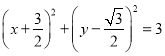 ,再利用三角代换得参数方程是
,再利用三角代换得参数方程是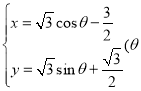 为参数),最后根据垂径定理求弦长
为参数),最后根据垂径定理求弦长
试题解析:(1)![]() 的极坐标化为直角坐标分别为
的极坐标化为直角坐标分别为![]() ,故直线
,故直线![]() 的斜率为
的斜率为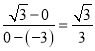 ,直线
,直线![]() 的方程为
的方程为![]() .由题意,当线段
.由题意,当线段![]() 时,线段
时,线段![]() 获得最小值,此时直线
获得最小值,此时直线![]() 的斜率为
的斜率为![]() ,所以直线
,所以直线![]() 的的方程为
的的方程为![]() ,联立
,联立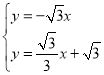 ,解得
,解得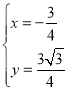 ,故所求点
,故所求点![]() 的直角坐标为
的直角坐标为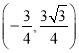 .
.
(2)因为![]() 的中点坐标为
的中点坐标为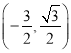 ,故以
,故以![]() 为直径的圆
为直径的圆![]() 直角坐标方程为
直角坐标方程为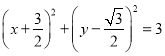 ,化为参数方程是
,化为参数方程是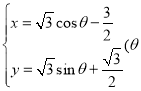 为参数),因为圆心
为参数),因为圆心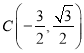 到直线
到直线![]() 的距离为
的距离为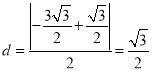 ,所以直线
,所以直线![]() 与圆
与圆![]() 相交所得的弦长为
相交所得的弦长为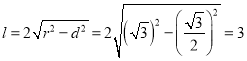 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:![]() ),其频率分布直方图如下:
),其频率分布直方图如下:

(1)估计旧养殖法的箱产量低于50![]() 的概率并估计新养殖法的箱产量的平均值;
的概率并估计新养殖法的箱产量的平均值;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量 | 箱产量 | 合计 | |
旧养殖法 | |||
新养殖法 | |||
合计 |
附:![]() ,其中
,其中![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参考数据:![]()


