题目内容

16．设椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$的焦点为F1、F2，直线L过点F1，且与椭圆相交于A，B两点，则△ABF2的周长为（　　）
A．9B．16C．20D．25

分析 利用椭圆的定义即可得出．

解答 解：∵椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$，则a=5．
∴△ABF2的周长=|AB|+|AF2|+|BF2|═|AF1|+|AF2|+|BF1|+|BF2|=2a+2a=4a=4×5=20．
故选：C．

点评 本题考查了椭圆的定义、三角形的周长，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
10．若sin（π+α）+cos（$\frac{π}{2}$+α）=-m，则cos（$\frac{3}{2}π$-α）+2sin（2π-α）的值为（　　）
A．-$\frac{2m}{3}$B．$\frac{2m}{3}$C．-$\frac{3m}{2}$D．$\frac{3m}{2}$
7．若关于x的函数y=（log${\;}_{\frac{1}{2}}$a）x是R上的减函数，则实数a的取值范围是（$\frac{1}{2}$，1）．
4．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点P（1，$\frac{3}{2}$），离心率e=$\frac{1}{2}$．
（Ⅰ）求椭圆C的方程
（Ⅱ）已知直线l：x=my+1与椭圆相交于A，B两点，记△ABP三条边所在直线的斜率的乘积为t，求t的最大值．
11．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右顶点，上顶点分别为M、N，过其左焦点F作直线l垂直于x轴，且与椭圆在第二象限交于点P，$\overrightarrow{MN}$=λ$\overrightarrow{OP}$
（1）求证：a=$\sqrt{b}$；
（2）若椭圆的弦AB过点E（2，0）并与坐标轴不垂直，设点A关于x轴的对称点A，直线A1B与x轴交于点R（5，0），求椭圆C的方程．
1．椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1的焦点为F1、F2，点P为这个椭圆上的动点，当∠F1PF2为钝角时，点P横坐标的取值范围是（-$\frac{4\sqrt{6}}{3}$，$\frac{4\sqrt{6}}{3}$）．
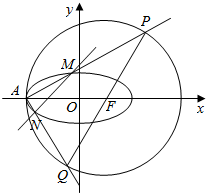8．已知A（-2，0）是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）与圆F：（x-c）2+y2=9的一个交点，且圆心F是椭圆的一个焦点，
（1）求椭圆C的方程；
（2）过F的直线交圆与P、Q两点，连AP、AQ分别交椭圆与M、N点，试问直线MN是否过定点？若过定点，则求出定点坐标；若不过定点，请说明理由．
5．关于x的一元二次方程x2-2ax+a+2=0在（1，3）内有两个不同实根，则a取值范围为（2，$\frac{11}{5}$）．
6．已知幂函数y=f（x）的图象过点$（2，\sqrt{2}）$，则f（9）=（　　）
A．3B．$\frac{1}{3}$C．9D．$\frac{1}{9}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网