题目内容
17.在△ABC中,角A、B、C对边分别是a、b、c,且满足2$\overrightarrow{AB}$•$\overrightarrow{AC}$=a2-(b-c)2(Ⅰ)求角A的大小;
(Ⅱ)若a=4$\sqrt{3}$,△ABC的面积为4$\sqrt{3}$,求b,c.
分析 (I)由题意可得2bccosA=a2-b2-c2-2bc,再由余弦定理求出cosA,从而确定A的大小;
(II)利用三角形的面积公式S=$\frac{1}{2}$bcsinA得bc=16;再由余弦定理得b2+c2+bc=48,联立求出b、c.
解答 解:(Ⅰ)由题意可得2bccosA=a2-b2-c2-2bc,
由余弦定理a2=b2+c2-2bccosA得4bccosA=-2bc,
∴cosA=-$\frac{1}{2}$,∵0<A<π,∴A=$\frac{2π}{3}$.
(Ⅱ)∵sinA=$\frac{\sqrt{3}}{2}$,cosA=-$\frac{1}{2}$,
∴S=$\frac{1}{2}bcsinA$=4$\sqrt{3}$,∴bc=16,
a2=b2+c2-2bccosA?b2+c2+bc=48,
∴b=c=4,
故b=4,c=4.
点评 本题考查余弦定理的应用,考查三角形的面积公式的应用,结合题设条件,利用余弦定理求出角A的大小是解答本题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
12.已知指数函数y=f(x)的图象过点($\frac{1}{2}$,$\frac{\sqrt{2}}{2}$),则log2f(2)的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -2 | D. | 2 |
2.下列方程中表示相同曲线的是( )
| A. | y=x,$\frac{y}{x}=1$ | B. | y=2x,$y=2\sqrt{x^2}$ | C. | |y|=|x|,$\sqrt{y}=\sqrt{x}$ | D. | |y|=|x|,y2=x2 |
6.已知幂函数y=f(x)的图象过点$(2,\sqrt{2})$,则f(9)=( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | 9 | D. | $\frac{1}{9}$ |
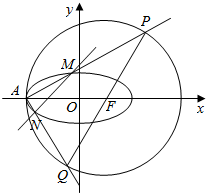 已知A(-2,0)是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与圆F:(x-c)2+y2=9的一个交点,且圆心F是椭圆的一个焦点,
已知A(-2,0)是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与圆F:(x-c)2+y2=9的一个交点,且圆心F是椭圆的一个焦点,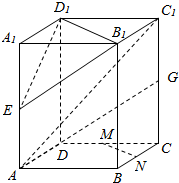 如图所示,在平行六面体ABCD-A1B1C1D1中,E.M.N.G分别是AA1,CD,CB,CC1的中点,求证:
如图所示,在平行六面体ABCD-A1B1C1D1中,E.M.N.G分别是AA1,CD,CB,CC1的中点,求证: