题目内容
设数列 前
前 项和为
项和为 ,且
,且 。其中
。其中 为实常数,
为实常数, 且
且 。
。
(1)求证: 是等比数列;
是等比数列;
(2)若数列 的公比满足
的公比满足 且
且 ,求
,求 的
的
通项公式;
(3)若 时,设
时,设 ,是否存在最大的正整数
,是否存在最大的正整数 ,使得对任意
,使得对任意 均有
均有 成立,若存在求出
成立,若存在求出 的值,若不存在请说明理由。
的值,若不存在请说明理由。
 前
前 项和为
项和为 ,且
,且 。其中
。其中 为实常数,
为实常数, 且
且 。
。(1)求证:
 是等比数列;
是等比数列;(2)若数列
 的公比满足
的公比满足 且
且 ,求
,求 的
的通项公式;
(3)若
 时,设
时,设 ,是否存在最大的正整数
,是否存在最大的正整数 ,使得对任意
,使得对任意 均有
均有 成立,若存在求出
成立,若存在求出 的值,若不存在请说明理由。
的值,若不存在请说明理由。解:(1)由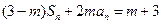 ,得
,得 ,两式相减,得
,两式相减,得 ,∴
,∴ ,∵
,∵ 是常数,且
是常数,且 ,
, ,
,
故 为不为0的常数,且由
为不为0的常数,且由 可得:
可得: ,
,
∴ 是等比数列。………4分
是等比数列。………4分
(2)由 ,且
,且 时,
时, ,
,
得 ,∴
,∴ 是以1为首项,
是以1为首项, 为公差的等差数列,
为公差的等差数列,
∴ ,故
,故 。………9分
。………9分
(3)由已知 ,∴
,∴
相减得: ,
,
∴ ,………12分
,………12分
 ,
, 递增,∴
递增,∴ ,
,
 对
对 均成立,∴
均成立,∴ ∴,又
∴,又 ,∴
,∴ 最大值为7。…14分
最大值为7。…14分
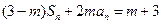 ,得
,得 ,两式相减,得
,两式相减,得 ,∴
,∴ ,∵
,∵ 是常数,且
是常数,且 ,
, ,
,故
 为不为0的常数,且由
为不为0的常数,且由 可得:
可得: ,
,∴
 是等比数列。………4分
是等比数列。………4分(2)由
 ,且
,且 时,
时, ,
,得
 ,∴
,∴ 是以1为首项,
是以1为首项, 为公差的等差数列,
为公差的等差数列,∴
 ,故
,故 。………9分
。………9分(3)由已知
 ,∴
,∴
相减得:
 ,
,∴
 ,………12分
,………12分 ,
, 递增,∴
递增,∴ ,
, 对
对 均成立,∴
均成立,∴ ∴,又
∴,又 ,∴
,∴ 最大值为7。…14分
最大值为7。…14分略

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
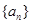 的前n项和为
的前n项和为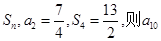 = ( )
= ( )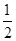



 n项和为Sn,且a3=5,S15="225."
n项和为Sn,且a3=5,S15="225." 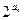 +2n,求数列{bn}的前n项和Tn.
+2n,求数列{bn}的前n项和Tn. 
 少年后,开始盈利?
少年后,开始盈利? 引进该设备若干年后,有两种处理方案:
引进该设备若干年后,有两种处理方案: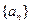 满足
满足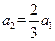 ,
,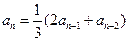 (
(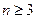 且
且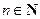 )
)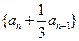 是常数列;
是常数列;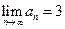 时,求数列
时,求数列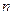 项和.
项和. 是等差数列
是等差数列 的前
的前 项之和,
项之和, ,
, ,则
,则 ( )
( )
 的前
的前 项和为
项和为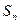 ,且
,且 对于
对于 为常数,且
为常数,且
 1)求证:数列
1)求证:数列 ,数列
,数列

 ,
,
 )(
)( ,
, ,求证:数列
,求证:数列


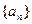 的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q
的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q 的前
的前 项和
项和 ,则
,则 的值为__ __
的值为__ __