题目内容
(理科做)直棱柱ABCD-A1B1C1D1中,AA1=AD=DC=2,BC=1,∠ADC=90°,下列结论:
①该直棱柱的体积一定是6
②用一平面去截直四棱柱,截面可能为三角形,四边形,五边形和六边形;
③M∈平面ABCD,D1M⊥平面A1C1D,则DM=2
;
④M∈平面ABCD,D1M⊥平面A1C1D,设D1M∩平面A1C1D=O,则
+
=
;
⑤M∈平面ABCD,D1M⊥平面A1C1D,设D1M∩平面A1C1D=O,则D1O:OM=1:2;
其中你认为正确的所有结论的序号是______.(写出所有正确命题的编号)
①该直棱柱的体积一定是6
②用一平面去截直四棱柱,截面可能为三角形,四边形,五边形和六边形;
③M∈平面ABCD,D1M⊥平面A1C1D,则DM=2
| 2 |
④M∈平面ABCD,D1M⊥平面A1C1D,设D1M∩平面A1C1D=O,则
| OC1 |
| OA1 |
| DO |
⑤M∈平面ABCD,D1M⊥平面A1C1D,设D1M∩平面A1C1D=O,则D1O:OM=1:2;
其中你认为正确的所有结论的序号是______.(写出所有正确命题的编号)
如图所示,
①由于底面积的大小不确定,因此其体积也不确定,故该直棱柱的体积一定是6不正确;
②用一平面去截直四棱柱,截面可能为三角形,四边形,五边形和六边形,正确;
③建立如图所示的空间直角坐标系,D1(0,0,0),A1(2,0,0),
C1(0,2,0),D(0,0,2).
则
=(-2,2,0),
=(-2,0,2),
∵M∈平面ABCD,可设M(x,y,2),则
=(x,y,2).
∵D1M⊥平面A1C1D,∴
,即
,解得
.
∴M(2,2,2),∴|DM|=
=2
,因此正确;
④M∈平面ABCD,D1M⊥平面A1C1D,设D1M∩平面A1C1D=O,
由③可知:M(2,2,2),点O为线段D1M的中点,即为等边三角形A1C1D的中心.
由重心定理可得:
+
=
,因此正确;
⑤M∈平面ABCD,D1M⊥平面A1C1D,设D1M∩平面A1C1D=O,则D1O:OM=1:2,由④可知不正确.
综上可知:只有②③④正确.
故答案为:②③④.
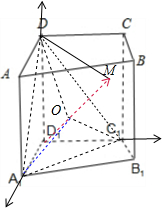
①由于底面积的大小不确定,因此其体积也不确定,故该直棱柱的体积一定是6不正确;
②用一平面去截直四棱柱,截面可能为三角形,四边形,五边形和六边形,正确;
③建立如图所示的空间直角坐标系,D1(0,0,0),A1(2,0,0),
C1(0,2,0),D(0,0,2).
则
| A1C1 |
| A1D |
∵M∈平面ABCD,可设M(x,y,2),则
| D1M |
∵D1M⊥平面A1C1D,∴
|
|
|
∴M(2,2,2),∴|DM|=
| 22+22+0 |
| 2 |
④M∈平面ABCD,D1M⊥平面A1C1D,设D1M∩平面A1C1D=O,
由③可知:M(2,2,2),点O为线段D1M的中点,即为等边三角形A1C1D的中心.
由重心定理可得:
| OC1 |
| OA1 |
| DO |
⑤M∈平面ABCD,D1M⊥平面A1C1D,设D1M∩平面A1C1D=O,则D1O:OM=1:2,由④可知不正确.
综上可知:只有②③④正确.
故答案为:②③④.


练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目