题目内容
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M为线段PB的中点.有以下四个命题:
①PA∥平面MOB;②MO∥平面PAC;③OC⊥平面PAC;
④平面PAC⊥平面PBC.其中正确的命题是( )
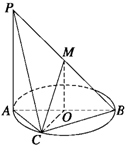
①PA∥平面MOB;②MO∥平面PAC;③OC⊥平面PAC;
④平面PAC⊥平面PBC.其中正确的命题是( )
| A.①和② | B.②和③ | C.③和④ | D.②和④ |

①∵PA?平面MOB,∴PA∥平面MOB不正确;
②由三角形的中位线定理可得MO∥PA,
又∵MO?平面PAC,PA?平面PAC,
∴MO∥平面PAC;
因此正确.
③∵OC与AC不垂直,因此OC⊥平面PAC不正确;
④∵PA⊥平面ABC,∴PA⊥BC.
由∠ACB是⊙O的直径AB所对的圆周角,
∴∠ACB=90°,即BC⊥AC.
又PA∩AC=A.
∴BC⊥平面PAC.
∴平面PAC⊥平面PBC.
因此④正确.
综上可知:其中正确的命题是②④.
故选:D.
②由三角形的中位线定理可得MO∥PA,
又∵MO?平面PAC,PA?平面PAC,
∴MO∥平面PAC;
因此正确.
③∵OC与AC不垂直,因此OC⊥平面PAC不正确;
④∵PA⊥平面ABC,∴PA⊥BC.
由∠ACB是⊙O的直径AB所对的圆周角,
∴∠ACB=90°,即BC⊥AC.
又PA∩AC=A.
∴BC⊥平面PAC.
∴平面PAC⊥平面PBC.
因此④正确.
综上可知:其中正确的命题是②④.
故选:D.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目