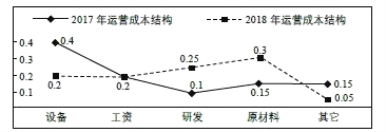
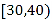题目内容
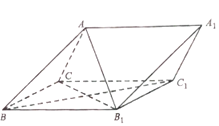
【题目】（题文）在三棱锥
中，
底面
，
，
且三棱锥的每个顶点都在球
的表面上，则球的表面积为 _______
【答案】
【解析】
根据题目所给的条件可得到相应的垂直关系，得到三角形ACD和三角形ABD均为直角三角形，有公共斜边AD，由直角三角形的性质得到AD中点为球心，进而得到球的半径和面积.
因为三棱锥
中，
底面
，所以
，又因为
，DC和CB相交于点C，故得到AB
面BCD，故得到AB垂直于BD，又因为DC垂直于面ABC，故DC垂直于AC，故三角形ACD和三角形ABD均为直角三角形，有公共斜边AD，取AD中点为O点，根据直角三角形斜边的中点为外心得到O到ABCD四个点的距离相等，故点O是球心，求得半径为3，由球的面积公式得到S=
.
故答案为：
.
练习册系列答案
相关题目
