题目内容
如图,有一边长为2米的正方形钢板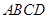 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线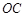 是以直线
是以直线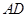 为对称轴,以线段
为对称轴,以线段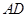 的中点
的中点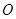 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.
(Ⅰ)请建立适当的直角坐标系,求阴影部分的边缘线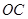 的方程;
的方程;
(Ⅱ)如何画出切割路径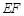 ,使得剩余部分即直角梯形
,使得剩余部分即直角梯形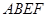 的面积最大?
的面积最大?
并求其最大值.
(I) 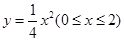 .(Ⅱ)当
.(Ⅱ)当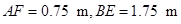 时,可使剩余的直角梯形的面积最大,其最大值为
时,可使剩余的直角梯形的面积最大,其最大值为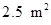 .
.
解析试题分析:(I)以 为原点,直线
为原点,直线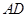 为
为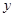 轴,建立如图所示的直角坐标系,
轴,建立如图所示的直角坐标系,
依题意
可设抛物线弧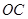 的方程为
的方程为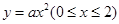
∵点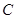 的坐标为
的坐标为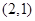 , ∴
, ∴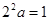 ,
,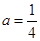
故边缘线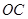 的方程为
的方程为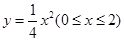 .
.
(Ⅱ)要使梯形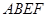 的面积最大,则
的面积最大,则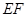 所在的直线必与抛物线弧
所在的直线必与抛物线弧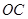 相切,设切点坐标为
相切,设切点坐标为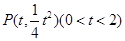 , ∵
, ∵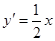 ,
,
∴直线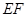 的的方程可表示为
的的方程可表示为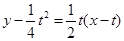 ,即
,即  , 由此可求得
, 由此可求得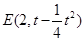 ,
,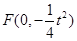 .
.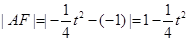 ,
,  ,
,
设梯形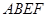 的面积为
的面积为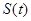 ,则
,则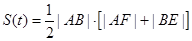
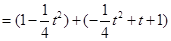
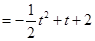
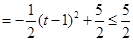 . ∴当
. ∴当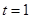 时,
时,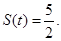
故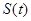 的最大值为
的最大值为 . 此时
. 此时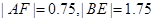 .
.
答:当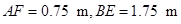 时,可使剩余的直角梯形的面积最大,其最大值为
时,可使剩余的直角梯形的面积最大,其最大值为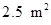 .
.
考点:本题主要考查抛物线在实际问题中的应用以及二次函数的图象和性质。
点评:解应用题常用的方法是依据题意建立等量关系,构造数学模型利用函数的性质进行求解,而有些应用题有明显的几何意义,可以考虑利用解析法根据题意建立适当的坐标系,构造曲线方程,利用曲线的性质进行求解.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
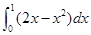 (2)
(2)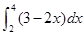
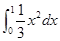 (4)
(4)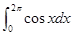
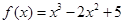 在区间
在区间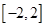 上的最值.
上的最值.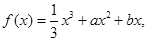 且
且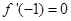
 的代数式表示
的代数式表示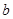 ;
; 的单调区间;
的单调区间; 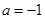 ,设函数
,设函数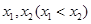 处取得极值,记点
处取得极值,记点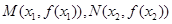 ,证明:线段
,证明:线段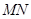 与曲线
与曲线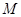 、
、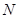 的公共点;
的公共点;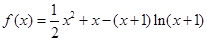
 的单调性;
的单调性;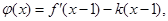 若函数
若函数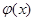 有两个零点
有两个零点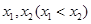 ,求证
,求证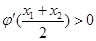
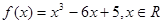 .
.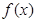 的极值点;
的极值点; 的方程
的方程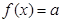 有3个不同实根,求实数a的取值范围.
有3个不同实根,求实数a的取值范围.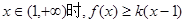 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.  在
在 上是单调递增函数,求实数
上是单调递增函数,求实数 的取值范围.
的取值范围.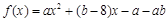
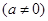 ,当
,当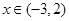 时,
时,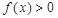 ;当
;当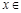 (
(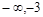 )
)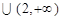 时,
时, .
.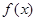 在[0,1]内的值域;
在[0,1]内的值域;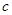 为何值时,不等式
为何值时,不等式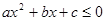 在[1,4]上恒成立.
在[1,4]上恒成立. .
. 时,求
时,求 的极值;
的极值; 时,求
时,求 及
及 ,恒有
,恒有 成立,求
成立,求 的取值范围
的取值范围