题目内容
(14分)设函数 .
.
(1)当 时,求
时,求 的极值;
的极值;
(2)当 时,求
时,求 的单调区间;
的单调区间;
(3)若对任意 及
及 ,恒有
,恒有 成立,求
成立,求 的取值范围
的取值范围
(Ⅰ)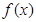 的极小值为
的极小值为 ,无极大值 .
,无极大值 .
(Ⅱ)当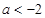 时,
时,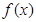 的递减区间为
的递减区间为 ;递增区间为
;递增区间为 .
.
当 时,
时,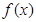 在
在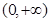 单调递减.
单调递减.
当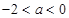 时,
时,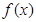 的递减区间为
的递减区间为 ;递增区间为
;递增区间为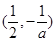 .
.
(Ⅲ) .
.
解析试题分析:(1)将a=0代入函数解析式中可知,函数的导数,然后运用导数的符号与单调性的关系求解单调区间,并得到极值。
(2)当a>0时,利用导函数,对于参数a,进而分类讨论研究其单调性,看开口和判别式得到。
(3)要证明不等式恒成立,只要利用第二问的结论根据最大值和最小值得到求解。
解:(Ⅰ)依题意,知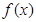 的定义域为
的定义域为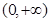 .
.
当 时,
时,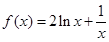 ,
,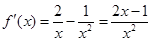 .
.
令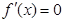 ,解得
,解得 .
.
当 时,
时,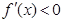 ;当
;当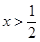 时,
时, .
.
又 ,
,
所以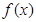 的极小值为
的极小值为 ,无极大值 . …………………………(4分)
,无极大值 . …………………………(4分)
(Ⅱ)
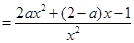
当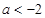 时,
时, ,
,
令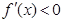 ,得
,得 或
或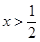 ,
,
令 ,得
,得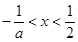 ;
;
当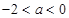 时,得
时,得 ,
,
令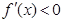 ,得
,得 或
或 ,
,
令 ,得
,得 ;
;
当 时,
时,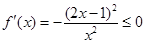 .
.
综上所述,当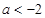 时,
时,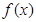 的递减区间为
的递减区间为 ;递增区间为
;递增区间为 .
.
当 时,
时,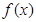 在
在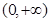 单调递减.
单调递减.
当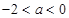 时,
时,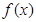 的递减区间为
的递减区间为 ;递增区间为
;递增区间为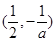 .
.
…………………………………(9分)
(Ⅲ)由(Ⅱ)可知,当 时,
时,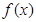 在
在 单调递减.
单调递减.
当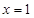 时,
时,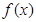 取最大值;当
取最大值;当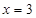 时,
时,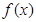 取最小值.
取最小值.
所以
 .………………(11分)
.………………(11分)
因为 恒成立,
恒成立,
所以 ,
,
整理得 .
.
又 所以
所以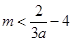 ,
,
又因为 ,得
,得 ,
,
所以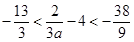
所以 . ……………………………………………………………(14分)
. ……………………………………………………………(14分)
考点:本试题主要考查了导数在研究函数中的运用。
点评:解决该试题的关键是对于含有参数的导数的符号的确定,需要分类讨论思想来得到。

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线 是以直线
是以直线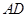 为对称轴,以线段
为对称轴,以线段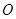 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.
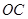 的方程;
的方程;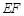 ,使得剩余部分即直角梯形
,使得剩余部分即直角梯形 的面积最大?
的面积最大?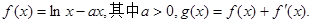
 的表达式;
的表达式;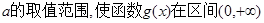 上是单调函数.
上是单调函数. ,其图象在点
,其图象在点 处的切线方程为
处的切线方程为 .
. 的值;
的值; 的单调区间,并求出
的单调区间,并求出 上的最大值.
上的最大值.
 .
. 的解集为
的解集为 且方程
且方程 的两实根为
的两实根为 .
. ,求
,求 的关系式;
的关系式; ,求证:
,求证: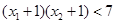 .
. 在
在 上是增函数,在
上是增函数,在 上是减函数.
上是减函数. 的解析式;
的解析式; 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,使得方程
,使得方程 在区间
在区间 上恰有两个相异实数根,若存在,求出
上恰有两个相异实数根,若存在,求出 ,直线
,直线 ,
, ,
, 围成图形的面积S.
围成图形的面积S. 函数
函数 的图象与
的图象与 的图象关于直线
的图象关于直线 对称,
对称, .
. 时,若对
时,若对 均有
均有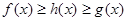 成立,求实数
成立,求实数 的取值范围;
的取值范围; 的图象与
的图象与 和
和 ,其中
,其中 .
. ;
; 时,关于
时,关于 的不等式
的不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.