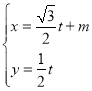题目内容
【题目】已知抛物线
的焦点
上一点
到焦点的距离为
.
（1）求
的方程；
（2）过
作直线
，交于
两点，若直线
中点的纵坐标为
，求直线
的方程.
【答案】（1）
（2）
【解析】
试题分析：（1）利用抛物线的定义，求出p，即可求C的方程；（2）利用点差法求出直线l的斜率，即可求直线l的方程
试题解析：（1）法一：抛物线
: 
的焦点
的坐标为
，
由已知
……………2分
解得
或
∵
，∴
∴的方程为.……4分
法二：抛物线: 的准线方程为
由抛物线的定义可知
解得…………………3分
∴的方程为.……………4分
（2）法一：由（1）得抛物线C的方程为
，焦点
设
两点的坐标分别为
，
则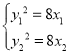
…………6分
两式相减。整理得
∵线段
中点的纵坐标为
∴直线
的斜率
……………………10分
直线的方程为
即……………12分
法二：由（1）得抛物线的方程为，焦点
设直线的方程为
由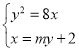
消去
，得
设两点的坐标分别为，
∵线段中点的纵坐标为
∴
解得
……………………………………10分
直线的方程为
即……………………………………12分
练习册系列答案
相关题目
