Question

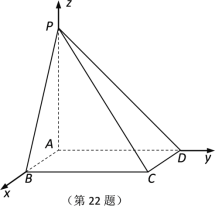
【题目】如图，棱锥P—ABCD的底面ABCD是矩形，PA⊥平面ABCD，PA=AD=2，BD=.

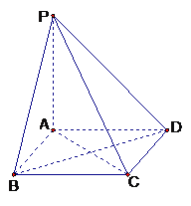
（1）求证：BD⊥平面PAC；

（2）求二面角P—CD—B余弦值的大小；

Answer 1

【答案】（1）证明见解析（2）

【解析】

（1）建立空间直角坐标系，再利用向量的数量积运算，证明线线垂直，从而证明线面垂直；

（2）建立空间直角坐标系，求平面的法向量，再利用数量积求向量的夹角即可得解.

解：（1）建立如图所示的直角坐标系，

则A（0，0，0）、D（0，2，0）、P（0，0，2）.

在Rt△BAD中，AD=2，BD=，

∴AB=2.∴B（2，0，0）、C（2，2，0），

∴

∵，即BD⊥AP，BD⊥AC，

又AP∩AC=A，

故BD⊥平面PAC.

（2）由（1）得.

设平面PCD的法向量为，则，

即，∴，故平面PCD的法向量可取为,

∵PA⊥平面ABCD，∴为平面ABCD的法向量.

设二面角P—CD—B的大小为，依题意可得，

故二面角P—CD—B余弦值的大小为.