题目内容
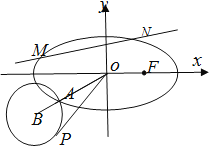
【题目】设A,B分别是双曲线![]() 的左右顶点,设过
的左右顶点,设过![]() 的直线PA,PB与双曲线分别交于点M,N,直线MN交x轴于点Q,过Q的直线交双曲线的于S,T两点,且
的直线PA,PB与双曲线分别交于点M,N,直线MN交x轴于点Q,过Q的直线交双曲线的于S,T两点,且![]() ,则
,则![]() 的面积( )
的面积( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
求得双曲线的左右顶点,设出直线PA,PB的方程,联立双曲线的方程,求得M,N的坐标,设![]() ,运用M,N,Q三点共线的条件,以及向量共线的条件,求得
,运用M,N,Q三点共线的条件,以及向量共线的条件,求得![]() ,设过Q的直线方程,联立双曲线方程,运用韦达定理和三角形的面积公式,计算可得所求值.
,设过Q的直线方程,联立双曲线方程,运用韦达定理和三角形的面积公式,计算可得所求值.
双曲线![]() 的左右顶点为
的左右顶点为![]() ,
,![]() ,
,![]() ,
,
可得直线PA的方程为![]() ,PB的方程为
,PB的方程为![]() ,
,
联立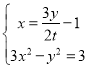 可得
可得![]() ,
,
解得![]() 或
或![]() ,
,
代入![]() 可得
可得![]() ,即有
,即有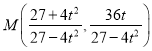 ,
,
联立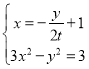 可得
可得![]() ,
,
解得![]() 或
或![]() ,
,
代入![]() ,可得
,可得![]() ,即
,即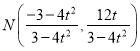 ,
,
设![]() ,由M,N,Q三点共线,可得
,由M,N,Q三点共线,可得![]() ,
,
即有![]() ,
,
将M,N的坐标代入化简可得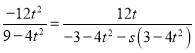 ,
,
解得![]() ,即
,即![]() ,
,
设过Q的直线方程为![]() ,
,
联立双曲线方程![]() ,可得
,可得![]() ,
,
设![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,
,![]() 恒成立,
恒成立,
![]() ,可得
,可得![]() ,代入韦达定理可得
,代入韦达定理可得![]() ,
,
解得![]() ,
,
可得![]()
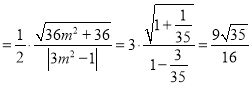 .
.
故选A.

练习册系列答案
相关题目
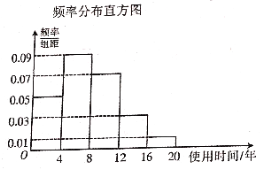
【题目】为了解一款电冰箱的使用时间和市民对这款电冰箱的购买意愿,研究人员对该款电冰箱进行了相应的抽样调查,得到数据的统计图表如下:
购买意愿市民年龄 | 不愿意购买该款电冰箱 | 愿意购买该款电冰箱 | 总计 |
40岁以上 | 600 | 800 | |
40岁以下 | 400 | ||
总计 | 800 |
(1)根据图中的数据,估计该款电冰箱使用时间的中位数;
(2)完善表中数据,并据此判断是否有![]() 的把握认为“愿意购买该款电冰箱“与“市民年龄”有关;
的把握认为“愿意购买该款电冰箱“与“市民年龄”有关;
(3)用频率估计概率,若在该电冰箱的生产线上随机抽取3台,记其中使用时间不低于4年的电冰箱的台数为![]() ,求
,求![]() 的期望.
的期望.
附:![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|