题目内容
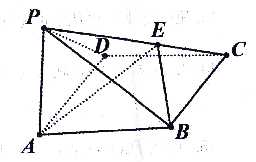
【题目】如图,在四棱锥![]() 中,底面ABCD为矩形,AC、BD交于点O,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
中,底面ABCD为矩形,AC、BD交于点O,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.

(1)求证:BD⊥平面PAC;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的大小.
的大小.
【答案】(1)见解析;(2)arccos![]()
【解析】
(1)证明PA⊥BD.PC⊥BD.即可证明BD⊥平面PAC.
(2)由PC⊥平面BDE得∠BEO为二面角 B﹣PC﹣A的平面角,在Rt△BEO中,即可求解二面角B﹣PC﹣A的大小.
证明:(1)∵PA⊥平面ABCD,BD平面ABCD
∴PA⊥BD.同理由PC⊥平面BDE,可证得PC⊥BD.
又PA∩PC=P,∴BD⊥平面PAC.
(2)由PC⊥平面BDE,故PC⊥OE,PC⊥BE则∠BEO为二面角 B﹣PC﹣A的平面角
由(1)知BO⊥AC∴ABCD为正方形∴AB=2,AC=2![]() ,故PC=3
,故PC=3
在Rt△BEO中,![]() 又
又![]() ,
,
∴cos∠EFO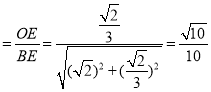
∴二面角B﹣PC﹣A的大小为arccos![]()

练习册系列答案
相关题目