题目内容
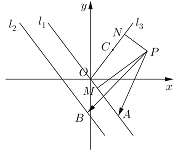
【题目】已知点![]() 在双曲线
在双曲线![]()
![]() (
(![]() ,
,![]() )上,且双曲线的一条渐近线的方程是
)上,且双曲线的一条渐近线的方程是![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)若过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 有两个不同的交点,求实数
有两个不同的交点,求实数![]() 的取值范围;
的取值范围;
(3)设(2)中直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两个不同的点,若以线段
两个不同的点,若以线段![]() 为直径的圆经过坐标原点,求实数
为直径的圆经过坐标原点,求实数![]() 的值.
的值.
【答案】(1)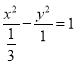 ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)要求双曲线的标准方程,必须找到关于![]() 的两个等式,题中一条渐近线方程为
的两个等式,题中一条渐近线方程为![]() ,说明
,说明![]() ,这是一个等式,点
,这是一个等式,点![]() 在双曲线上,那么此点坐标适合双曲线方程,代入进去又可得到一个等式,这样可解得
在双曲线上,那么此点坐标适合双曲线方程,代入进去又可得到一个等式,这样可解得![]() ;(2)直线与双曲线有两个不同的交点,直接把直线方程与双曲线方程联立方程组,此方程组有两解,方法是消去一个元
;(2)直线与双曲线有两个不同的交点,直接把直线方程与双曲线方程联立方程组,此方程组有两解,方法是消去一个元![]() ,得到关于
,得到关于![]() 的二次方程,此方程是二次方程有两个不等的实根,则
的二次方程,此方程是二次方程有两个不等的实根,则![]() ;(3)题设条件说明
;(3)题设条件说明![]() ,如果设
,如果设![]() ,则有
,则有![]() ,
,![]() 可用
可用![]() 表示出来,而
表示出来,而![]() 在(2)中可用
在(2)中可用![]() 表示出来,代入刚才的等式,得到
表示出来,代入刚才的等式,得到![]() 的方程,可解得
的方程,可解得![]() .
.
试题解析:(1)由题知,有
解得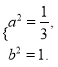
因此,所求双曲线![]() 的方程是
的方程是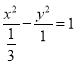 .
.
(2)∵直线![]() 过点
过点![]() 且斜率为
且斜率为![]() ,
,
∴直线![]() :
:![]() .
.
联立方程组![]() 得
得![]() .
.
又直线![]() 与双曲线
与双曲线![]() 有两个不同交点,
有两个不同交点,
∴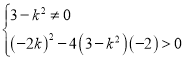
解得![]() .
.
(3)设交点为![]() ,由(2)可得
,由(2)可得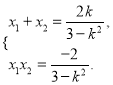
又以线段![]() 为直径的圆经过坐标原点,
为直径的圆经过坐标原点,
因此,![]() 为坐标原点).
为坐标原点).
于是,![]() 即
即![]() ,
,![]() ,
,
![]() ,解得
,解得![]() .
.
又![]() 满足
满足![]() ,且
,且![]() ,
,
所以,所求实数![]() .
.

练习册系列答案
相关题目