题目内容
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值;
的距离的最大值;
(Ⅱ)若曲线![]() 上的所有点都在直线
上的所有点都在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)将直线![]() 的极坐标方程化为普通方程
的极坐标方程化为普通方程![]() ,进而由圆的参数方程得曲线
,进而由圆的参数方程得曲线![]() 上的点到直线
上的点到直线![]() 的距离,
的距离, ![]()
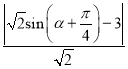 ,利用三角函数求最值即可;
,利用三角函数求最值即可;
(2)曲线![]() 上的所有点均在直线
上的所有点均在直线![]() 的下方,即为对
的下方,即为对![]() ,有
,有![]() 恒成立,即
恒成立,即![]() (其中
(其中![]() )恒成立,进而得
)恒成立,进而得![]() .
.
试题解析:
(1)直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
曲线![]() 上的点到直线
上的点到直线![]() 的距离,
的距离,
![]()
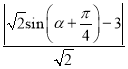 ,
,
当![]() 时,
时, 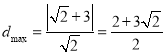 ,
,
即曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值为
的距离的最大值为![]() .
.
(2)∵曲线![]() 上的所有点均在直线
上的所有点均在直线![]() 的下方,
的下方,
∴对![]() ,有
,有![]() 恒成立,
恒成立,
即![]() (其中
(其中![]() )恒成立,
)恒成立,
∴![]() .
.
又![]() ,∴解得
,∴解得![]() ,
,
∴实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】甲、乙两所学校高三年级分别有1 200人,1 000人,为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 3 | 4 | 8 | 15 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 15 | x | 3 | 2 |
乙校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 1 | 2 | 8 | 9 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 10 | 10 | y | 3 |
则x,y的值分别为( )
(A)、12,7 (B)、 10,7 (C)、 10,8 (D)、 11,9