题目内容
若f(x)是R上周期为5的奇函数,且满足f(1)=1,f(2)=2,则f(3)-f(4)=( )
| A.-1 | B.1 | C.-2 | D.2 |
A
∵f(x)是R上周期为5的奇函数
∴f(3)=f(3-5)=f(-2)=-f(2)=-2
f(4)=f(4-5)=f(-1)=-f(1)=-1,
f(3)-f(4)=-2+1=-1
∴f(3)=f(3-5)=f(-2)=-f(2)=-2
f(4)=f(4-5)=f(-1)=-f(1)=-1,
f(3)-f(4)=-2+1=-1

练习册系列答案
相关题目
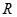 上函数
上函数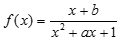 为奇函数.
为奇函数.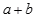 的值;
的值;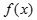 的值域.
的值域.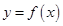 为偶函数,当
为偶函数,当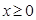 时,
时,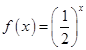 ,则不等式
,则不等式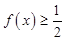 的解集为______.
的解集为______.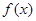 满足
满足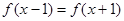 ,且在
,且在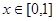 时,
时,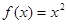 ,则关于
,则关于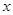 的方程
的方程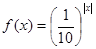 在
在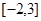 上的根的个数是
上的根的个数是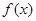 是定义在R上的奇函数.当x<0时,
是定义在R上的奇函数.当x<0时,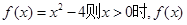 的解析式为 ;不等式f(x)<0的解集为 .
的解析式为 ;不等式f(x)<0的解集为 .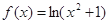 的图象大致是( )
的图象大致是( )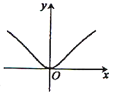
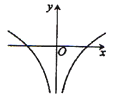
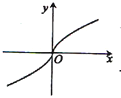
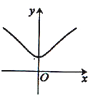
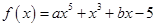 ,若
,若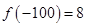 ,那么
,那么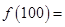 ______
______