Question

已知直线l：x-y+4=0与圆C：（x-1）²+（y-1）²=2，则C上各点到l的距离的最小值为______．

Answer 1

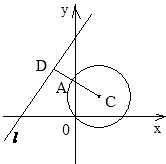
如图可知：过圆心作直线l：x-y+4=0的垂线，则AD长即为所求；
∵圆C：（x-1）²+（y-1）²=2的圆心为C（1，1），半径为

2

，
点C到直线l：x-y+4=0的距离为d=

|1-1+4|

2

=2

2

，
∴AD=CD-AC=2

2

-

2

=

2

，
故C上各点到l的距离的最小值为

2

．
故答案为：

2