题目内容
17.已知函数f(x)=lnx+(x-b)2(b∈R)在区间$[{\frac{1}{2},2}]$上存在单调递增区间,则实数b的取值范围是( )| A. | $({-∞,\frac{3}{2}})$ | B. | $({-∞,\frac{9}{4}})$ | C. | (-∞,3) | D. | $({-∞,\sqrt{2}})$ |
分析 利用导函数得到不等式恒成立,然后求解b的范围.
解答 解:∵函数f(x)在区间$[{\frac{1}{2},2}]$上存在单调增区间,
∴函数f(x)在区间$[{\frac{1}{2},2}]$上存在子区间使得不等式f′(x)>0成立.
$f'(x)=\frac{1}{x}+2({x-b})=\frac{{2{x^2}-2bx+1}}{x}$,
设h(x)=2x2-2bx+1,则h(2)>0或$h({\frac{1}{2}})>0$,
即8-4b+1>0或$\frac{1}{2}-b+1>0$,
得$b<\frac{9}{4}$.
故选:B.
点评 本题考查函数的导数的综合应用,不等式的解法,考查计算能力.

练习册系列答案
相关题目
5.方程|x|+|y|=1表示的曲线是( )
| A. |  | B. | 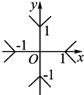 | C. | 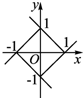 | D. | 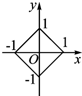 |
12.若集合A={x|-1<x<2},B={x|(2x+1)(3-x)<0},则A∩B是( )
| A. | {x|2<x<3} | B. | {x|-$\frac{1}{2}$<x<2} | C. | {x|-1$<x<-\frac{1}{2}$} | D. | {x|-1$<x<\frac{1}{2}$或2<x<3} |
6.命题p:?x>0,总有x2-1≥0,则?p为( )
| A. | ?x0≤0,使得x2-1<0 | B. | ?x0>0,使得x2-1<0 | ||
| C. | ?x>0,总有x2-1<0 | D. | ?x≤0,总有x2-1<0 |