题目内容
已知直线Ax+By+C=0(其中A2+B2=C2,c≠0)与圆x2+y2=4交于M,N,O是坐标原点,则| OM |
| ON |
分析:由题设条件求出圆心到直线的距离,解三角形求出∠MON=120°,又两向量的模是2,由内积公式求出两向量的内积.
解答: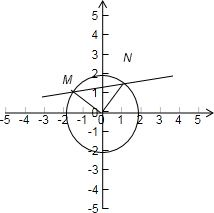 解:由题设条件,圆的圆心为(0,0)半径为2,圆心到直线Ax+By+C=0(其中A2+B2=C2,c≠0)
解:由题设条件,圆的圆心为(0,0)半径为2,圆心到直线Ax+By+C=0(其中A2+B2=C2,c≠0)
圆心到直线Ax+By+C=0(其中A2+B2=C2,c≠0)的距离d=
=
=1
故直线Ax+By+C=0圆的一条半径的中点,由此知∠OMN=∠ONM=30°
所以∠MON=120°
则
•
=2×2×cos∠MON=-2
故应填-2.
 解:由题设条件,圆的圆心为(0,0)半径为2,圆心到直线Ax+By+C=0(其中A2+B2=C2,c≠0)
解:由题设条件,圆的圆心为(0,0)半径为2,圆心到直线Ax+By+C=0(其中A2+B2=C2,c≠0)圆心到直线Ax+By+C=0(其中A2+B2=C2,c≠0)的距离d=
| |C| | ||
|
| |C| |
| |C| |
故直线Ax+By+C=0圆的一条半径的中点,由此知∠OMN=∠ONM=30°
所以∠MON=120°
则
| OM |
| ON |
故应填-2.
点评:本题考查直线与圆的位置关系以及向量的内积公式,把直线与圆的位置关系结合起来考查是本题的一个亮点,设计新颖.

练习册系列答案
相关题目
已知直线Ax+By+C=0(其中A2+B2=C2,C≠0)与圆x2+y2=4交于M,N,O是坐标原点,则
•
=( )
| OM |
| ON |
| A、-1 | B、-1 | C、-2 | D、2 |