题目内容

已知直线ax+by+c=0与圆O：x2+y2=4相交于A、B两点，且|
AB
|=2
3
，则
OA
•
OB
=
-2
-2
．
分析：由题意，可先作出图象，根据图象，得到
AB
=
OB
-
OA
，两边乘方，即可得到关于
OA
•
OB
的方程，解之即可
解答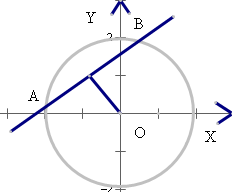：解：由题知，圆O：x2+y2=4半径为2，|
AB
|=2
3

如图，
AB
=
OB
-
OA

两边平方得
AB
2=
OB
2-2
OB
•
OA
+
OA
2
所以12=4+4-2
OB
•
OA
，解得
OA
•
OB
=-2
故答案为-2
点评：本题考查直线与圆相交的性质及向量数量积的运算，解答的关键是找出向量三角形，建立方程求值
练习册系列答案
相关题目
已知直线ax+by+c=0（abc≠0）与圆x2+y2=1相离，则以三条边长分别为|a|，|b|，|c|所构成的三角形的形状是
 
．
已知直线Ax+By+C=0（其中A2+B2=C2，C≠0）与圆x2+y2=4交于M，N，O是坐标原点，则
OM
•
ON
=（　　）
A、-1B、-1C、-2D、2
（2013•济南一模）已知直线ax+by+c=0与圆O：x2+y2=1相交于A，B两点，且|AB|=
3
，则
OA
•
OB
的值是（　　）
已知直线ax+by+c=0（abc≠0）与圆x2+y2=1相离，则三条边长分别为|a|、|b|、|c|的三角形（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网