题目内容
(2013•济南一模)已知直线ax+by+c=0与圆O:x2+y2=1相交于A,B两点,且|AB|=
,则
•
的值是( )
| 3 |
| OA |
| OB |
分析:直线与圆有两个交点,知道弦长、半径,不难确定∠AOB的大小,即可求得
•
的值.
| OA |
| OB |
解答:解:取AB的中点C,连接OC,|AB|=
,则AC=
,OA=1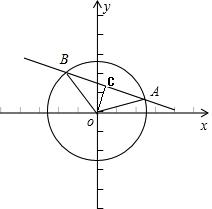
∴sin (
∠ AOB)=sin∠AOC=
=
所以:∠AOB=120°
则
•
=1×1×cos120°=-
.
故选A.
| 3 |
| ||
| 2 |

∴sin (
| 1 |
| 2 |
| AC |
| OA |
| ||
| 2 |
所以:∠AOB=120°
则
| OA |
| OB |
| 1 |
| 2 |
故选A.
点评:本题主要考查了直线和圆的方程的应用,以及向量的数量积公式的应用,同时考查了计算能力,属于基础题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
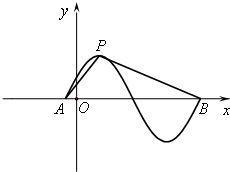 (2013•济南一模)函数y=sin(
(2013•济南一模)函数y=sin(