题目内容
【题目】已知公差不为0的等差数列{an}的前n项和为Sn ， 且S3=9，a1 ， a3 ， a7成等比数列．
（1）求数列{an}的通项公式；
（2）数列{bn}满足bn=（an﹣1）2n ， 求数列{bn}的前n项和Tn ．
【答案】
（1）解：等差数列{an}公差为d，首项为a1，
∵a1，a3，a7成等比数列．
∴a32=a1a7，
即（a1+2d）2=a1（a1+6d），
化简得d= 
a1，或d=0（舍去）．
当d= a1，
由等差数列S3=3a2，
∴a2=3，得a1=2，d=1．
∴an=a1+（n﹣1）d=2+（n﹣1）=n+1，即an=n+1，
数列{an}的通项公式an=n+1
（2）解：由（1）可知：an=n+1，
bn=（an﹣1）2n=（n+1﹣1）2n=n2n，
∴bn=n2n，
数列{bn}的前n项和Tn，Tn=2+2×22+3×23+…+n×2n，
2Tn=22+2×23+3×24+…+n×2n+1，
两式相减：得﹣Tn=2+22+22+…+2n﹣n×2n+1，
=2n+1﹣2﹣n×2n+1，
∴Tn=（n﹣1）2n+1+2．
数列{bn}的前n项和Tn，Tn=（n﹣1）2n+1+2
【解析】（1）根据条件可知a32=a1a7 ， 即（a1+2d）2=a1（a1+6d），d和a1的关系，S3=3a2 ， 即可求得a1和d，数列{an}的通项公式；（2）求得数列{bn}的通项公式，采用乘以公比“错位相减法”，即可求得数列{bn}的前n项和Tn ．
【考点精析】认真审题，首先需要了解等差数列的通项公式（及其变式）(通项公式：
或
)，还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系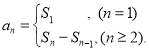
)的相关知识才是答题的关键．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
