题目内容
【题目】如图,在△ABC中,角A,B,C所对的边分别为a,b,c,( ![]() a﹣sinC)cosB=sinBcosC,b=4
a﹣sinC)cosB=sinBcosC,b=4 ![]() .
. 
(1)求角B的大小;
(2)D为BC边上一点,若AD=2,S△DAC=2 ![]() ,求DC的长.
,求DC的长.
【答案】
(1)解:∵( ![]() a﹣sinC)cosB=sinBcosC,
a﹣sinC)cosB=sinBcosC,
∴ ![]() acosB=sinCcosB+sinBcosC=sin(B+C)=sinA,
acosB=sinCcosB+sinBcosC=sin(B+C)=sinA,
在△ABC中,由正弦定理可得: ![]() ,
,
∴ ![]() =1,
=1,
∴tanB= ![]() =
= ![]() ,B∈(0,π),
,B∈(0,π),
∴B= ![]()
(2)解:∵S△DAC=2 ![]() =
= ![]() sin∠DAC,
sin∠DAC,
∴sin∠DAC= ![]() ,
,
∵0<∠DAC< ![]() ,
,
∴∠DAC= ![]() .
.
在△DAC中,DC2= ![]() ﹣2×
﹣2× ![]() cos
cos ![]() =28.
=28.
∴DC=2 ![]()
【解析】(1)由( ![]() a﹣sinC)cosB=sinBcosC,利用和差公式、三角形内角和定理、诱导公式可得
a﹣sinC)cosB=sinBcosC,利用和差公式、三角形内角和定理、诱导公式可得 ![]() acosB=sinA,再利用正弦定理、同角三角函数基本关系式即可得出.(2)利用三角形面积计算公式、余弦定理即可得出.
acosB=sinA,再利用正弦定理、同角三角函数基本关系式即可得出.(2)利用三角形面积计算公式、余弦定理即可得出.
【考点精析】关于本题考查的正弦定理的定义和余弦定理的定义,需要了解正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能得出正确答案.
才能得出正确答案.

【题目】宜昌市拟在2020年点军奥体中心落成后申办2022年湖北省省运会,据了解,目前武汉,襄阳,黄石等申办城市因市民担心赛事费用超支而准备相继退出,某机构为调查宜昌市市民对申办省运会的态度,选了某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
(1)根据已知数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过![]() 的前提下认为不同年龄与支持申办省运会无关?
的前提下认为不同年龄与支持申办省运会无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.
附: 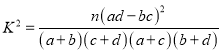 ,
, ![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |


