题目内容
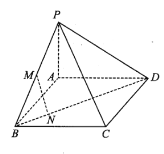
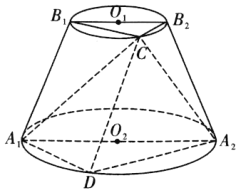
【题目】如图,圆台![]() 的轴截面为等腰梯形
的轴截面为等腰梯形![]() ,
,![]() ,
,![]() ,
,![]() ,圆台
,圆台![]() 的侧面积为
的侧面积为![]() .若点C,D分别为圆
.若点C,D分别为圆![]() ,
,![]() 上的动点且点C,D在平面
上的动点且点C,D在平面![]() 的同侧.
的同侧.
(1)求证:![]() ;
;
(2)若![]() ,则当三棱锥
,则当三棱锥![]() 的体积取最大值时,求多面体
的体积取最大值时,求多面体![]() 的体积.
的体积.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由圆台侧面积求出上下底半径,计算圆台的高,计算![]() ,由直角三角形性质得
,由直角三角形性质得![]() ;
;
(2)三棱锥![]() 的高就是
的高就是![]() ,表示出三棱锥
,表示出三棱锥![]() 的体积,求出最大值时
的体积,求出最大值时![]() ,
,![]() ,多面体
,多面体![]() 分为三棱锥
分为三棱锥![]() 和四棱锥
和四棱锥![]() ,分别计算体积后相加即得.
,分别计算体积后相加即得.
解:(1)设![]() ,
,![]() 的半径分别为
的半径分别为![]() ,
,![]() ,
,
因为圆台的侧面积为![]() ,
,
所以![]() ,可得
,可得![]() .
.
因此,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
如图,连接线段![]() ,
,![]() ,
,![]() ,
,
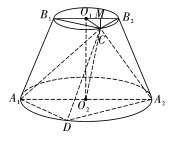
在圆台![]() 中,
中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() .
.
又![]() ,所以在
,所以在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() ,故
,故![]() ,即
,即![]() .
.
(2)由题意可知,三棱锥![]() 的体积为
的体积为![]() ,
,
又在直角三角形![]() 中,
中,![]() ,
,
所以当且仅当![]() ,
,
即点D为弧![]() 的中点时,
的中点时,![]() 有最大值
有最大值![]() .
.
过点C作![]() 交
交![]() 于点M,
于点M,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() ,则点C到平面
,则点C到平面![]() 的距离
的距离![]() ,
,
所以四棱锥![]() 的体积
的体积![]() .
.
综上,当三棱锥![]() 体积最大值时,
体积最大值时,
多面体![]()

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目