题目内容
【题目】培养某种水生植物需要定期向培养植物的水中加入物质
，已知向水中每投放1个单位的物质，
（单位：天）时刻后水中含有物质的量增加
，
与的函数关系可近似地表示为关系可近似地表示为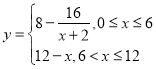
.根据经验，当水中含有物质的量不低
时，物质才能有效发挥作用.
（1）若在水中首次投放1个单位的物质，计算物质能持续有效发挥作用几天？
（2）若在水中首次投放1个单位的物质，第8天再投放1个单位的物质，试判断第8天至第12天，水中所含物质的量是否始终不超过
，并说明理由.
【答案】（1）6天.（2）第8天至第12天，水中所含物质
的量始终不超过
.见解析
【解析】
（1）由题可知
，分类讨论求解满足
时的
的范围，即可得出在水中首次投放1个单位的物质，物质能持续有效发挥作用的天数；
（2）根据已知求出函数解析式
，利用基本不等式即可求得当
时，
，从而得出结论.
解：（1）由题意，(单位：天)时刻后水中含有物质的量为：
，
由于当水中含有物质的量不低
时，物质才能有效发挥作用，
即需，
则当
时，
且当
时，
，
解得：
，
所以若在水中首次投放1个单位的物质，物质能持续有效发挥作用的时间为：8-2=6天.
（2）设第
天水中所含物质的量为
，
则
，
，
当且仅当
，即
时，等号成立，
即当时，，
所以第8天至第12天，水中所含物质的量始终不超过.
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
