题目内容
【题目】已知动圆过定点![]() ,且与直线
,且与直线![]() 相切.
相切.
(1)求动圆的圆心轨迹![]() 的方程;
的方程;
(2)是否存在直线![]() ,使
,使![]() 过点(0,1),并与轨迹
过点(0,1),并与轨迹![]() 交于
交于![]() 两点,且满足
两点,且满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【答案】(1)![]() (2)直线
(2)直线![]() 存在,其方程为
存在,其方程为![]() .
.
【解析】
(1)设![]() 为动圆圆心,根据圆
为动圆圆心,根据圆![]() 与直线
与直线![]() 相切可得
相切可得![]() ,结合抛物线的定义知,点
,结合抛物线的定义知,点![]() 的轨迹为抛物线,从而解决问题;
的轨迹为抛物线,从而解决问题;
(2)对“是否存在性”问题,先假设存在,设直线![]() 的方程为
的方程为![]() ,与抛物线方程联立结合根的判别式求出
,与抛物线方程联立结合根的判别式求出![]() 的范围,再利用向量垂直求出
的范围,再利用向量垂直求出![]() 值,看它们之间是否矛盾,没有矛盾就存在,否则不存在.
值,看它们之间是否矛盾,没有矛盾就存在,否则不存在.
(1)如图,
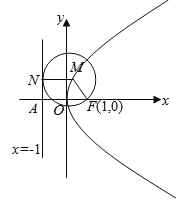
设![]() 为动圆圆心,
为动圆圆心,![]() ,
,
过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,由题意知:
,由题意知:![]()
即动点![]() 到定点
到定点![]() 与到定直线
与到定直线![]() 的距离相等,
的距离相等,
由抛物线的定义知,点![]() 的轨迹为抛物线,
的轨迹为抛物线,
其中![]() 为焦点,
为焦点,![]() 为准线,
为准线,
![]() 动圆圆心的轨迹方程为
动圆圆心的轨迹方程为![]() ;
;
(2)由题可设直线![]() 的方程为
的方程为![]()
由![]() 得
得![]() ;
;
△![]() ,
,
解得![]() 或
或![]()
设![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]()
由![]() ,即
,即![]() ,
,
得![]()
解得![]() 或
或![]() (舍去),
(舍去),
![]() 直线
直线![]() 存在,其方程为
存在,其方程为![]() .
.

【题目】点P为两直线l1:3x+4y﹣2=0和l2:2x+y+2=0的交点.
(1)求过P点且与直线3x﹣2y+4=0平行的直线方程;
(2)求过原点且与直线l1和l2围成的三角形为直角三角形的直线方程.
【题目】规定投掷飞镖3次为一轮,3次中至少两次投中8环以上的为优秀.现采用随机模拟实验的方法估计某人投掷飞镖的情况:先由计算器产生随机数0或1,用0表示该次投镖未在8环以上,用1表示该次投镖在8环以上;再以每三个随机数作为一组,代表一轮的结果.例如:“101”代表第一次投镖在8环以上,第二次投镖未在8环以上,第三次投镖在8环以上,该结果代表这一轮投镖为优秀:"100”代表第一次投镖在8环以上,第二次和第三次投镖均未在8环以上,该结果代表这一轮投镖为不优秀.经随机模拟实验产生了如下10组随机数,据此估计,该选手投掷飞镖两轮,至少有一轮可以拿到优秀的概率是( )
101 | 111 | 011 | 101 | 010 | 100 | 100 | 011 | 111 | 001 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()