题目内容
10.求a+a3+a5+…+a2n-1的值.分析 分a=1与a≠1两种情况讨论,当a=1时即求n个1的和,当a≠1时利用等比数列的求和公式计算即得结论.
解答 解:对a的值进行讨论:
当a=1时,a+a3+a5+…+a2n-1=n;
当a≠1时,a+a3+a5+…+a2n-1=$\frac{a(1-{a}^{2n})}{1-{a}^{2}}$.
点评 本题考查数列的求和,考查分类讨论的思想,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
19.函数f(x)=$\frac{{x}^{2}-1}{({x}^{2}+1)^{2}}$的值域为( )
| A. | (0,$\frac{1}{4}$] | B. | [-1,$\frac{1}{4}$] | C. | (0,$\frac{1}{8}$] | D. | [-1,$\frac{1}{8}$] |
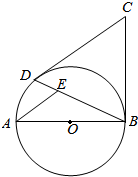 如图,切线CD、CB分别与⊙O相交于点D、B,AB为⊙O的直径,AE∥CD交BD于点E,若AB=BC,则sin∠BAE的值为$\frac{3}{5}$.
如图,切线CD、CB分别与⊙O相交于点D、B,AB为⊙O的直径,AE∥CD交BD于点E,若AB=BC,则sin∠BAE的值为$\frac{3}{5}$.