题目内容
函数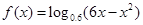 的单调递增区间为( )
的单调递增区间为( )
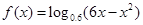 的单调递增区间为( )
的单调递增区间为( )A.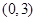 | B.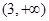 | C. | D. |
C
分析:由已知中函数f(x)的解析式,先确定函数的定义域,进而根据二次函数和对数函数的性质,分别判断内,外函数的单调性,进而根据复合函数“同增异减”的原则,得到答案.
解答:解:函数f(x)=log0.6(6x-x2)的定义域为(0,6)
令t=6x-x2,则y=log0.6t
∵y=log0.6t为减函数
t=6x-x2的单调递增区间是(0,3),单调递减区间是[3,6)
故函数f(x)=log0.6(6x-x2)的单调递增区间是(3,6)
故选C
点评:本题考查的知识点是二次函数的图象和性质,对数函数的单调区间,复合函数的单调性,其中复合函数单调性“同增异减”的原则,是解答本题的关键,解答时易忽略函数的定义域而错解为:(3,+∞)
解答:解:函数f(x)=log0.6(6x-x2)的定义域为(0,6)
令t=6x-x2,则y=log0.6t
∵y=log0.6t为减函数
t=6x-x2的单调递增区间是(0,3),单调递减区间是[3,6)
故函数f(x)=log0.6(6x-x2)的单调递增区间是(3,6)
故选C
点评:本题考查的知识点是二次函数的图象和性质,对数函数的单调区间,复合函数的单调性,其中复合函数单调性“同增异减”的原则,是解答本题的关键,解答时易忽略函数的定义域而错解为:(3,+∞)

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
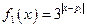 ,
,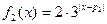 ,
,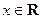 ,
,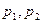 为常
为常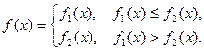
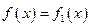 对所有实数成立的充要条件(用
对所有实数成立的充要条件(用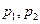 表示);
表示);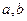 为两实数,
为两实数,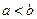 且
且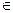
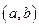 ,若
,若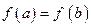
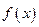 在区间
在区间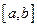 上的单调增区间的长度和为
上的单调增区间的长度和为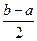 (闭区间
(闭区间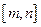 的长度定义为
的长度定义为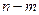 ).
). ,
, 为实数.
为实数. 时,判断函数
时,判断函数 的奇偶性,并说明理由;
的奇偶性,并说明理由; 时,指出函数
时,指出函数 ,使得
,使得 上的最大值为2.若存在,求出
上的最大值为2.若存在,求出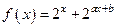 ,且f(1)=
,且f(1)=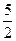 ,f(2)=
,f(2)=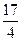 .(1)求
.(1)求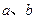 ;(2)判断
;(2)判断 f(x)的奇偶性;(3)试判断函数在
f(x)的奇偶性;(3)试判断函数在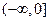 上的单调性,并证明。
上的单调性,并证明。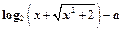 为奇
为奇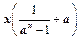 为偶函数,证明你的结论。
为偶函数,证明你的结论。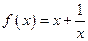 在区间
在区间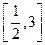 上的最小值为
上的最小值为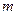 ,最大值为
,最大值为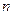 ,则
,则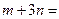
 ,
, ,设
,设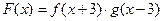 ,且函数
,且函数 的零点均在区间
的零点均在区间 内,则
内,则 的最小值为____▲_____.
的最小值为____▲_____.