题目内容
已知函数f(x)是R上的增函数,A(0,-3),B(3,1)是其图象上的两点,那么不等式-3<f(x+1)<1的解集的补集是( )
| A.(-1,2) | B.(1,4) |
| C.(―∞,-1)∪[4,+∞) | D.(―∞,-1]∪[2,+∞) |
D
分析: f(0)<f(x+1)<f(3).根据f(x)为R上的增函数,
可得0<x+1<3,解出x.
解答:解:由题意知f(0)=-3,f(3)=1.-3<f(x+1)<1
即f(0)<f(x+1)<f(3).又f(x)为R上的增函数,
∴0<x+1<3.∴-1<x<2,所以不等式-3<f(x+1)<1的解集的补集是(―∞,-1]∪[2,+∞)
故选D.
点评:本题考查函数的单调性的应用,以及绝对值不等式的解法,体现了转化的数学思想.
可得0<x+1<3,解出x.
解答:解:由题意知f(0)=-3,f(3)=1.-3<f(x+1)<1
即f(0)<f(x+1)<f(3).又f(x)为R上的增函数,
∴0<x+1<3.∴-1<x<2,所以不等式-3<f(x+1)<1的解集的补集是(―∞,-1]∪[2,+∞)
故选D.
点评:本题考查函数的单调性的应用,以及绝对值不等式的解法,体现了转化的数学思想.

练习册系列答案
相关题目
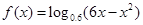 的单调递增区间为( )
的单调递增区间为( )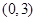
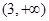


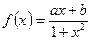 是定义在(-1,1)上的奇函数,且
是定义在(-1,1)上的奇函数,且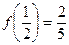
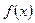 的解析式
的解析式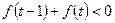 的
的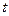 的范围
的范围 是定义在R上的奇函数,
是定义在R上的奇函数, ,在
,在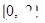 上
上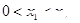 <4且
<4且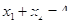 ,则
,则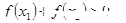 ;
; ,则
,则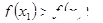 ;
; 内恰有四个不同的解
内恰有四个不同的解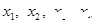 ,则
,则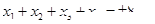 。其中正确的有
。其中正确的有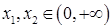 ,都有
,都有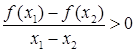 ”的是( )
”的是( )  B
B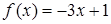
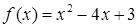 D
D 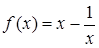
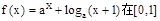 上的最大值和最小值之和为a,则a的值为 ( )
上的最大值和最小值之和为a,则a的值为 ( )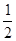
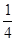
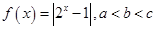 且
且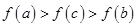 ,则下列结论中,必成立的是( )
,则下列结论中,必成立的是( )



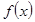 是周期为2的奇函数,当
是周期为2的奇函数,当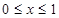 时,
时,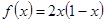 ,
,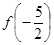 =( )
=( )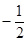
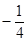
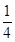

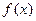 在R上是偶函数,若当
在R上是偶函数,若当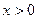 时,有
时,有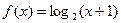 ,则
,则 .
.