题目内容
【题目】已知t为实数,函数![]() ,其中
,其中![]()
(1)若![]() ,求
,求![]() 的取值范围。
的取值范围。
(2)当![]() 时,
时,![]() 的图象始终在
的图象始终在![]() 的图象的下方,求t的取值范围;
的图象的下方,求t的取值范围;
(3)设![]() ,当
,当![]() 时,函数
时,函数![]() 的值域为
的值域为![]() ,若
,若![]() 的最小值为
的最小值为![]() ,求实数a的值.
,求实数a的值.
【答案】(1)![]() (2)t>1(3)a=
(2)t>1(3)a=![]()
【解析】
(1)根据对数函数的图像与性质化简即可求解;
(2)构造函数h(x)=f(x)-g(x),根据对数函数的图象和性质可得,根据二次函数的性质求出t的取值范围即可;
(3)先判断函数y=|f(x)|的单调性,令|2loga(2x+2)|=2,即可得到n-m的最小值.
解:(1)由题意得函数g(x)在(0,+∞)上是减函数,
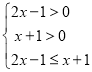 ,解得
,解得![]() ,则x的取值范围是
,则x的取值范围是![]() ;
;
(2)由题意设h(x)=f(x)-g(x)=2loga(2x+t-2)-logax<0在x∈[1,4]恒成立,
∴2loga(2x+t-2)<logax,
∵0<a<1,x∈[1,4],
∴只需要2x+t-2>![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
∴![]() ,
,
令![]() ,
,
∴![]() ,
,
∴t的取值范围是t>1,
(3)∵t=4,0<a<1,
∴函数y=|f(x)|=|2loga(2x+2)|在(-1,-![]() )上单调递减,在(-
)上单调递减,在(-![]() ,+∞)上单调递增,
,+∞)上单调递增,
∵当x∈[m,n]时,函数y=|f(x)|的值域为[0,2],且f(-![]() )=0,
)=0,
∴![]() (等号不同时取到),
(等号不同时取到),
令|2loga(2x+2)|=2,得![]() ,
,
又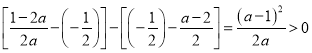 ,
,
∴![]() ,
,
∴n-m的最小值为![]() ,
,
∴a=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某城市理论预测2010年到2014年人口总数与年份的关系如下表所示
年份2010+x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据,求出y关于x的线性回归方程;
(2) 据此估计2015年该城市人口总数。