题目内容
【题目】在同一坐标系中,函数y=ax+a与y=ax的图象大致是( )
A.  B.
B. 
C.  D.
D. 
【答案】B
【解析】
一方面,函数y=ax横过点(0,1)且在a>1时递增,在0<a<1时递减;另一方面再结合函数y=ax+a与y轴的交点为(0,a)作出判断.
解:∵函数y=ax横过点(0,1)且在a>1时递增,在0<a<1时递减,而函数y=ax+a与y轴的交点为(0,a),
因此,A中、由y=ax的图象递增得知a>1,由函数y=ax+a与y轴的交点(0,a)得知a<1,矛盾;
C中、由y=ax的图象递减得知0<a<1,由函数y=ax+a与y轴的交点(0,a)得知a>1,矛盾;
D中、由y=ax的图象递减得知0<a<1,函数y=ax+a递减得知a<0,矛盾;
故选:B.

练习册系列答案
相关题目
【题目】某种商品在![]() 天内每件的销售价格
天内每件的销售价格![]() (元)与时间
(元)与时间![]() (
(![]() )(天)的函数关系满足函数
)(天)的函数关系满足函数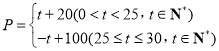 ,该商品在
,该商品在![]() 天内日销售量
天内日销售量![]() (件)与时间
(件)与时间![]() (
(![]() )(天)之间满足一次函数关系如下表:
)(天)之间满足一次函数关系如下表:
第 |
|
|
|
|
|
|
|
|
|
(1)根据表中提供的数据,确定日销售量![]() 与时间
与时间![]() 的一次函数关系式;
的一次函数关系式;
(2)求该商品的日销售金额的最大值并指出日销售金额最大的一天是![]() 天中的第几天,(日销售金额
天中的第几天,(日销售金额![]() 每件的销售价格
每件的销售价格![]() 日销售量)
日销售量)