题目内容
【题目】定义在![]() 上的函数
上的函数![]() ,若已知其在
,若已知其在![]() 内只取到一个最大值和一个最小值,且当
内只取到一个最大值和一个最小值,且当![]() 时函数取得最大值为
时函数取得最大值为![]() ;当
;当![]() ,函数取得最小值为
,函数取得最小值为![]() .
.
(1)求出此函数的解析式;
(2)是否存在实数![]() ,满足不等式
,满足不等式![]() ?若存在,求出
?若存在,求出![]() 的范围(或值),若不存在,请说明理由;
的范围(或值),若不存在,请说明理由;
(3)若将函数![]() 的图像保持横坐标不变纵坐标变为原来的
的图像保持横坐标不变纵坐标变为原来的![]() 得到函数
得到函数![]() ,再将函数
,再将函数![]() 的图像向左平移
的图像向左平移![]() 个单位得到函数
个单位得到函数![]() ,已知函数
,已知函数![]() 的最大值为
的最大值为![]() ,求满足条件的
,求满足条件的![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)存在
;(2)存在![]() ,见解析;(3)最小值为
,见解析;(3)最小值为![]()
【解析】
(1)利用最大值和最小值可确定![]() ,又
,又![]() ,可求得
,可求得![]() ;根据
;根据![]() ,结合
,结合![]() 的范围可求得
的范围可求得![]() ,从而得到解析式;(2)首先保证原式有意义可得到
,从而得到解析式;(2)首先保证原式有意义可得到![]() ;根据二次函数性质可确定
;根据二次函数性质可确定![]() ,
,![]() ;由函数在
;由函数在![]() 上递增可确定
上递增可确定![]() ,解不等式求得结果;(3)根据三角函数伸缩和平移变化得到
,解不等式求得结果;(3)根据三角函数伸缩和平移变化得到![]() 和
和![]() ;由复合函数单调性可确定当
;由复合函数单调性可确定当![]() 取最大值时,需
取最大值时,需![]() 与
与![]() 同时取得,从而求得
同时取得,从而求得![]() ,根据
,根据![]() 确定最小值.
确定最小值.
(1)![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
解得:![]() ,
,![]() ,又
,又![]()
![]()
![]()
(2)![]() 满足
满足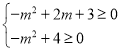 ,解得:
,解得:![]()
![]()
![]()
同理![]()
由(1)知函数在![]() 上递增
上递增
若有![]()
只需要:![]() ,即
,即![]() 成立即可
成立即可
![]() 存在
存在![]() ,使
,使![]() 成立
成立
(3)由题意知:![]() ,
,![]()
![]() 函数
函数![]() 与函数
与函数![]() 均为单调增函数,且
均为单调增函数,且![]() ,
,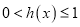
![]() 当且仅当
当且仅当![]() 与
与![]() 同时取得才有函数的最大值为
同时取得才有函数的最大值为![]()
由![]() 得:
得:![]() ,
,![]()
则![]()
![]()
![]() ,
,![]()
又![]()
![]() 的最小值为
的最小值为![]()

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目