题目内容
【题目】已知椭圆C： 
（a＞b＞0）的离心率为 
，直线l：y=x+2与以原点为圆心、椭圆C的短半轴为半径的圆O相切．
（1）求椭圆C的方程；
（2）过椭圆C的左顶点A作直线m，与圆O相交于两点R，S，若△ORS是钝角三角形，求直线m的斜率k的取值范围．
【答案】
（1）
解：由题意可得e= 
= 
，
又圆O的方程为x2+y2=b2，
因为直线l：x﹣y+2=0与圆O相切，
b= 
，由a2=3c2=3（a2﹣b2），即a2=3．
所以椭圆C的方程为 
（2）
解：由（1）得知圆的方程为x2+y2=2．A（﹣ 
，0），直线m 的方程为：y=k（x+ ）．
设R（x1，y1），S（x2，y2），由 
得 
，
由△=12k4﹣4（1+k2）（3k2﹣2）＞0的﹣ 
＜k＜ …①
因为△ORS是钝角三角形，∴ 
= 
= 
．
…②
由A、R、S三点不共线，知k≠0． ③
由①、②、③，得直线m的斜率k的取值范围是（﹣ 
，0）∪（0， ）
【解析】（1）求得圆O的方程，运用直线和相切的条件：d=r，求得b，再由离心率公式和a，b，c的关系，可得a，进而得到椭圆方程；（2）先设出点R，S的坐标，利用△ORS是钝角三角形，求得 
=x1x2+y1y2＜0，从而求出斜率k的取值范围
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
【题目】某种商品在
天内每件的销售价格
（元）与时间
（
）（天）的函数关系满足函数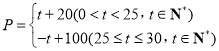
，该商品在天内日销售量
（件）与时间（）（天）之间满足一次函数关系如下表：
第 |
|
|
|
|
|
|
|
|
|
（1）根据表中提供的数据，确定日销售量与时间的一次函数关系式；
（2）求该商品的日销售金额的最大值并指出日销售金额最大的一天是天中的第几天,（日销售金额
每件的销售价格
日销售量）
