题目内容
动圆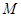 经过定点
经过定点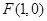 ,且与直线
,且与直线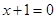 相切。
相切。
(1)求圆心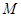 的轨迹
的轨迹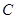 方程;
方程;
(2)直线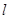 过定点
过定点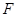 与曲线
与曲线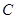 交于
交于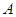 、
、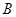 两点:
两点:
①若 ,求直线
,求直线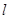 的方程;
的方程;
②若点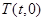 始终在以
始终在以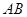 为直径的圆内,求
为直径的圆内,求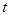 的取值范围。
的取值范围。
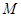 经过定点
经过定点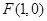 ,且与直线
,且与直线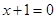 相切。
相切。(1)求圆心
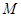 的轨迹
的轨迹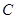 方程;
方程;(2)直线
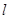 过定点
过定点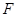 与曲线
与曲线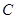 交于
交于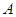 、
、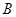 两点:
两点:①若
 ,求直线
,求直线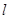 的方程;
的方程;②若点
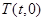 始终在以
始终在以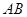 为直径的圆内,求
为直径的圆内,求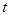 的取值范围。
的取值范围。(1) ;(2)
;(2)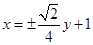 ,
, 。
。
 ;(2)
;(2)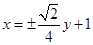 ,
, 。
。试题分析:(1)由题意:
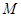 到点
到点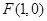 距离与
距离与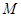 到直线
到直线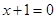 距离相等,所以点
距离相等,所以点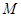 的轨迹是以
的轨迹是以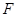 为焦点,直线
为焦点,直线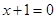 为准线的抛物线,其方程为
为准线的抛物线,其方程为
(2)①设直线
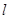 :
: ,代入抛物线方程得:
,代入抛物线方程得: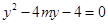
设
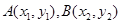 则
则
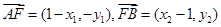 由
由 得
得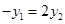 ,
, 代入
 解得:
解得: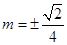 即所求直线方程为
即所求直线方程为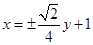 。
。 ②
 ,由题意:
,由题意: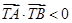
即
 ,
, ,化简得:
,化简得: 对于任意的
对于任意的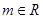 恒成立。
恒成立。 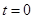 满足
满足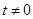 ,则
,则 且
且 ,解得
,解得 。综上知,
。综上知,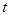 的取值范围为
的取值范围为 。
。点评:(1)求轨迹方程的一般方法:直接法、定义法、相关点法、参数法、交轨法、向量法等。本题求轨迹方程用到的是定义法。用定义法求轨迹方程的关键是条件的转化——转化成某一已知曲线的定义条件。(2)直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
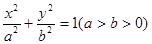 的离心率
的离心率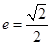 ,左焦点为
,左焦点为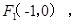 右焦点为
右焦点为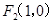 ,短轴两个端点为
,短轴两个端点为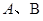 .与
.与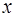 轴不垂直的直线
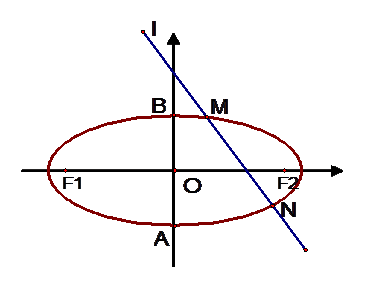
轴不垂直的直线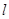 与椭圆C交于不同的两点
与椭圆C交于不同的两点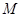 、
、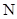 ,记直线
,记直线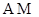 、
、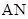 的斜率分别为
的斜率分别为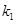 、
、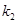 ,且
,且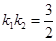 .
.
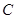 的方程;
的方程;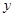 轴相交于定点,并求出定点坐标.
轴相交于定点,并求出定点坐标. 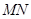 的中点
的中点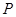 落在
落在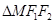 内(包括边界)时,求直线
内(包括边界)时,求直线 是以
是以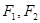 为左、右焦点的双曲线
为左、右焦点的双曲线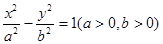 左支上一点,且满足
左支上一点,且满足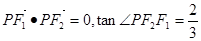 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )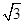
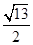
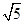
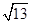
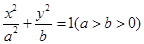 的左、右焦点分别为
的左、右焦点分别为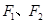 ,离心率
,离心率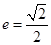 ,
, 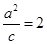 .
.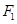 的直线
的直线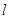 与该椭圆交于
与该椭圆交于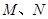 两点,且
两点,且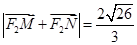 ,求直线
,求直线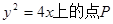 到抛物线的准线距离为d1,到直线
到抛物线的准线距离为d1,到直线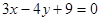 的距离为d2,则d1+d2的最小值是
的距离为d2,则d1+d2的最小值是 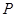 在曲线
在曲线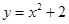 上,点
上,点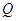 在曲线
在曲线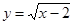 上,则
上,则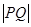 的最小值等于 .
的最小值等于 .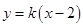
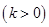 与抛物线
与抛物线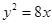 相交于
相交于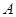 、
、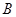 两点,
两点,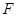 为抛物线的焦点,若
为抛物线的焦点,若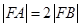 ,则
,则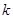 的值为 。
的值为 。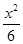 -
-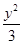 =1的渐近线与圆(x-3)2+y2=r2(r>0)相切,则r=( )
=1的渐近线与圆(x-3)2+y2=r2(r>0)相切,则r=( )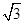
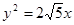 的焦点是双曲线C的一个焦点,且双曲线经过点
的焦点是双曲线C的一个焦点,且双曲线经过点 ,又知直线
,又知直线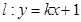 与双曲线C相交于A、B两点.
与双曲线C相交于A、B两点.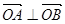 ,求实数k值.
,求实数k值.