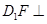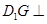题目内容
如图,正方形ABCD所在的平面与三角形CDE所在的平面交于CD,AE⊥平面CDE,且AB=2AE.

(1)求证:AB∥平面CDE;
(2)求证:平面ABCD⊥平面ADE.

(1)求证:AB∥平面CDE;
(2)求证:平面ABCD⊥平面ADE.
(1)见解析(2)见解析
(1)正方形ABCD中,AB∥CD,
又AB?平面CDE,CD?平面CDE,
所以AB∥平面CDE.
(2)因为AE⊥平面CDE,且CD?平面CDE,
所以AE⊥CD,又正方形ABCD中,CD⊥AD,且AE∩AD=A,
AE、AD?平面ADE,所以CD⊥平面ADE,
又CD?平面ABCD,
所以平面ABCD⊥平面ADE.
又AB?平面CDE,CD?平面CDE,
所以AB∥平面CDE.
(2)因为AE⊥平面CDE,且CD?平面CDE,
所以AE⊥CD,又正方形ABCD中,CD⊥AD,且AE∩AD=A,
AE、AD?平面ADE,所以CD⊥平面ADE,
又CD?平面ABCD,
所以平面ABCD⊥平面ADE.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
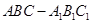 中,D、E分别是BC和
中,D、E分别是BC和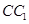 的中点,已知AB=AC=AA1=4,ÐBAC=90°.
的中点,已知AB=AC=AA1=4,ÐBAC=90°.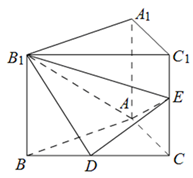
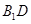 ⊥平面
⊥平面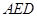 ;
;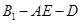 的余弦值;
的余弦值;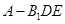 的体积.
的体积.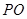 中,已知
中,已知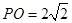 ,
, 的直径
的直径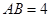 ,点
,点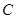 在底面圆周上,且
在底面圆周上,且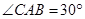 ,
,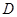 为
为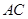 的中点.
的中点.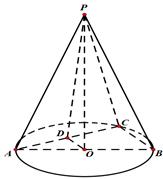
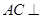 平面
平面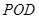 ;
;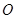 到面
到面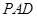 的距离.
的距离.
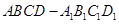 中,
中,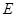 、
、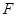 为棱
为棱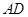 、
、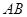 的中点.
的中点.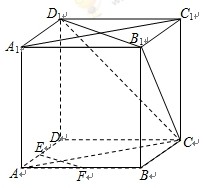
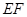 ∥平面
∥平面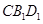 ;
;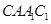 ⊥平面
⊥平面
 平面PBC ②平面
平面PBC ②平面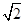 .
.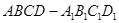 ,点
,点 ,
,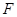 ,
,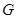 分别是线段
分别是线段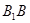 ,
,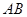 和
和 上的动点,观察直线
上的动点,观察直线 与
与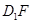 ,
,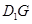 .给出下列结论:
.给出下列结论: