Question

（本小题满分12分）已知：以点为圆心的圆与x轴交于
点O，A，与y轴交于点O，B，其中O为原点。
(Ⅰ) 求证：⊿OAB的面积为定值；
(Ⅱ) 设直线y=-2x+4与圆C交于点M，N，若OM=ON,求圆C的方程。

Answer 1

解：(Ⅰ)因为圆C过原点O， 
设圆C的方程是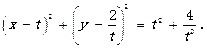    令x=0,得y₁ =0，；
令y=0，得x₁=0,x₂="2t" . 
即⊿OAB的面积为定值。  5分；
(Ⅱ)方法一：垂直平分线段MN。
直线OC的方程是 解得 t=2或t=-2。
当t=2时，圆心C的坐标为（2,1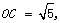），此时C到直线y=-2x+4的距离
圆C与直线y=-2x+4相交于两点。
当t=-2时，圆心C的坐标为（-2,-1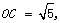），此时C到直线y=-2x+4的距离此时圆C与直线y=-2x+4不相交，
所以t=-2不符合题意，舍去。所以，圆C的方程为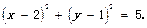        12分
方法二：可用解方程法，结果相同。过程从略。

解析