题目内容
证明:(1)连结OC,∴∠OAC=∠OCA,
又∵CA是∠BAF的角平分线,∴∠OAC=∠FAC,
∴∠FAC=∠ACO,∴OC∥AD,
∵CD⊥AF,∴CD⊥OC,即DC是⊙O的切线.
(2)连结BC,在Rt△ACB中,CM⊥AB,
∴CM2=AM·MB,
又∵DC是⊙O的切线,∴DC2=DF·DA,
易知△AMC≌△ADC,∴DC=CM,
∴AM·MB=DF·DA
解析

练习册系列答案
相关题目
点P在正方体ABCD﹣A1B1C1D1的底面ABCD所在平面上,E是A1A的中点,且∠EPA=∠D1PD,则点P的轨迹是( )
| A.直线 | B.圆 | C.抛物线 | D.双曲线 |
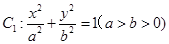 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C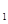 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线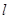 恰好与圆
恰好与圆 相切.
相切.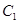 的离心率;
的离心率; 的最大值为49,求椭圆C
的最大值为49,求椭圆C 点是圆
点是圆 上的动点,过点
上的动点,过点
 的两条切线,切点分别为
的两条切线,切点分别为 ,切线
,切线 分别交
分别交 轴于
轴于 两点.
两点. 面积的最小值;
面积的最小值; 被圆
被圆 在点
在点 ;若不存在,说明理由.
;若不存在,说明理由.
 为圆心的圆与x轴交于
为圆心的圆与x轴交于 的左焦点,A为右顶点,上下虚轴端点B、C,若FB交CA于D,且
的左焦点,A为右顶点,上下虚轴端点B、C,若FB交CA于D,且 ,则此双曲线的离心率为( ).
,则此双曲线的离心率为( ). B.
B. C.
C.  D.
D.
 ,
, 且圆心在
且圆心在 轴
轴
 上的圆的方程.
上的圆的方程. =0相切.
=0相切.