题目内容
(本小题满分12分)光线l过点P(1,-1),经y轴反射后与圆C:(x-4)2+(y- 4)2=1
4)2=1
相切,求光线l所在的直线方程.
解:设l与y轴的交点(即反射点)为Q,点P关于y轴的对称点为P′(-1,-1).由
光学知识可知直线P′Q为反射线所在的直线,且为圆C的切线. ………………………2分
设P′Q的方程为y+1 =k(x+1),即kx-y+k-1="0," …………………………………4分
=k(x+1),即kx-y+k-1="0," …………………………………4分
由于圆心C(4,4)到P′Q的距离等于半径长,
∴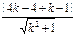 =1.解得k=
=1.解得k=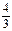 或k=
或k=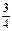 .…………………………………8分
.…………………………………8分
由l与P′Q关于y轴对称可得l的斜率为-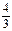 或-
或-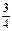 ,…………………………10分
,…………………………10分
∴光线l所在的直线方程为y+1=-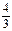 (x-1)或y+1=-
(x-1)或y+1=-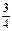 (x-1),
(x-1),
即4x+3y-1=0或3x+4y+1="0." ………………………………12分
解析

练习册系列答案
相关题目
双曲线 的渐近线与圆
的渐近线与圆 相切,则双曲线离心率为( ).
相切,则双曲线离心率为( ).
A. | B.2 | C. | D.3 |
 和
和 .
. 上,求圆的方程。
上,求圆的方程。 ,
, 内接于此圆,
内接于此圆, 点的坐标
点的坐标 ,
, 为坐标原点.
为坐标原点. ,求直线
,求直线 的方程;
的方程;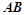 与直线
与直线 的倾斜角互补,求证:直线
的倾斜角互补,求证:直线 N(1,0)的距离的比为。
N(1,0)的距离的比为。 为圆心的圆与x轴交于
为圆心的圆与x轴交于 ,1)直线
,1)直线 :
: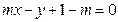
 ,直线
,直线 点;
点; 时,求m的值。
时,求m的值。 与圆O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.
与圆O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.
 ;
; .
. .求 圆C的方程.
.求 圆C的方程.