题目内容
4.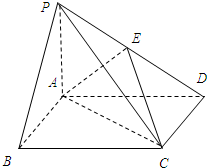 在如图所示四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是正方式,PA=AB=1,E是PD上的点,PB∥平面AEC,
在如图所示四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是正方式,PA=AB=1,E是PD上的点,PB∥平面AEC,(Ⅰ)确定点E的位置并证明AE⊥PC
(Ⅱ)求三棱锥P-AEC的体积.
分析 (Ⅰ)连接BD交AC于O点,连接EO,利用线面平行的性质,可得点E的位置;利用直线与平面垂直的判定,证明AE⊥PC
(Ⅱ)利用体积公式求三棱锥P-AEC的体积.
解答 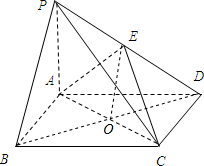 解:(Ⅰ)连接BD交AC于O点,连接EO,
解:(Ⅰ)连接BD交AC于O点,连接EO,
因为PB∥平面AEC,平面PBD∩平面ACE=OE,
所以EO∥PB,
因为O为BD中点,
所以E为PD中点;
因为E为PD的中点,PA=AB=AD,
所以AE⊥PD,
因为PA⊥底面ABCD,
所以PA⊥CD,
因为CD⊥AD∩AD=A,
所以CD⊥平面PAD,
所以AE⊥平面PCD,
所以AE⊥PC
(Ⅱ)三棱锥P-AEC的体积=$\frac{1}{2}$VP-ACD=$\frac{1}{4}{V}_{P-ABCD}$=$\frac{1}{4}×\frac{1}{3}×PA×AB×AD$=$\frac{1}{12}$.
点评 本题考查直线与平面平行的性质,直线与平面垂直的判定,考查三棱锥P-AEC的体积,考查学生的逻辑思维能力,是中档题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
14.在一张纸上画一个圆,圆心O,并在圆外设一点F,折叠纸圆上某点落于F点,设该点为M,抹平纸片,折痕AB,连接MO(或者OM)并延长交于AB于P,则P点轨迹为( )
| A. | 椭圆 | B. | 双曲线 | C. | 抛物线 | D. | 直线 |
12.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知sinA-sinB=$\frac{1}{3}$sinC,3b=2a,2≤a2+ac≤18,设△ABC的面积为S,p=$\sqrt{2}$a-S,则p的最小值是( )
| A. | $\frac{5\sqrt{2}}{9}$ | B. | $\frac{7\sqrt{2}}{9}$ | C. | $\sqrt{2}$ | D. | $\frac{9\sqrt{2}}{8}$ |
16.已知函数f(x)=x${\;}^{-\frac{1}{2}}$-log3x,若x0是函数y=f(x)的零点,且0<x1<x0,则f(x1)( )
| A. | 恒为正值 | B. | 等于0 | C. | 恒为负值 | D. | 不大于0 |
14.下列有关命题的说法正确的是( )
| A. | 命题“若x2=1,则x=1”的否命题为“若x2≠1,则x≠1” | |
| B. | 命题“若x=y,则sinx=siny”的逆命题为真命题 | |
| C. | 命题“?x0∈R,x${\;}_{0}^{2}$+x0+1=0”的否定是“?x∈R,x2+x+1<0” | |
| D. | 命题“若am2<bm2,则a<b”的逆命题是真命题 |