题目内容
8.已知椭圆C的左右焦点坐标分别是(-2,0),(2,0),离心率$\frac{\sqrt{2}}{2}$,经过P(1,1)的直线L与椭圆C交于不同的两点A,B.(1)求椭圆C的方程;
(2)若点P为弦AB的中点,求直线L的方程及弦AB的长度.
分析 (1)由题意可得,c=2,e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,可得a,由a,b,c的关系,即可得到b,进而得到椭圆方程;
(2)设弦的端点为A(x1,y1)、B(x2,y2),代入椭圆方程,作差,并由中点坐标公式,可得直线斜率k,从而求出弦所在的直线方程.再由椭圆方程,运用韦达定理和弦长公式即可得到弦长.
解答 解:(1)由题意可得,c=2,e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
解得a=2$\sqrt{2}$,b=2,
即有椭圆方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1;
(2)设弦的端点为A(x1,y1)、B(x2,y2),
代入椭圆方程,得
x12+2y12=8①,x22+2y22=8②;
①-②,得(x1+x2)(x1-x2)+2(y1+y2)(y1-y2)=0;
由中点坐标$\frac{{x}_{1}+{x}_{2}}{2}$=1,$\frac{{y}_{1}+{y}_{2}}{2}$=1,代入上式,得
(x1-x2)+2(y1-y2)=0,
∴直线斜率为k=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=-$\frac{1}{2}$,
所求弦的直线方程为:y-1=-$\frac{1}{2}$(x-1),
即x+2y-3=0.
由x+2y-3=0和椭圆方程x2+2y2=8,
可得3x2-6x-7=0,
可得x1+x2=2,x1x2=-$\frac{7}{3}$,
可得|AB|=$\sqrt{1+\frac{1}{4}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\frac{\sqrt{5}}{2}$•$\sqrt{4+\frac{28}{3}}$=$\frac{5\sqrt{6}}{3}$.
点评 本题考查椭圆方程的求法和圆锥曲线中点坐标公式的运用,通过作差的方法,求得直线斜率k的应用模型,属于中档题.

 发散思维新课堂系列答案
发散思维新课堂系列答案| A. | 恒为正值 | B. | 等于0 | C. | 恒为负值 | D. | 不大于0 |
| A. | ($\frac{2}{19}$,$\frac{2}{15}$) | B. | (0,$\frac{15}{2}$) | C. | (0,$\frac{2}{17}$) | D. | (0,$\frac{17}{2}$) |
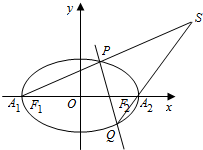 如图所示,已知椭圆C:$\frac{x^2}{4}$+y2=1左、右端点分别为A1,A2,过定点(1,0)的动直线与椭圆C交于P,Q两点.直线A1P与A2Q交于点S.
如图所示,已知椭圆C:$\frac{x^2}{4}$+y2=1左、右端点分别为A1,A2,过定点(1,0)的动直线与椭圆C交于P,Q两点.直线A1P与A2Q交于点S.