题目内容
【题目】为了研究一种昆虫的产卵数![]() 和温度
和温度![]() 是否有关,现收集了7组观测数据列于下表中,并作出了如图的散点图.
是否有关,现收集了7组观测数据列于下表中,并作出了如图的散点图.
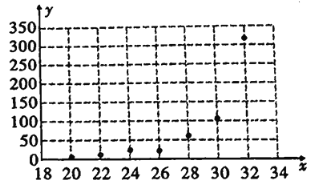
温度 | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
产卵数 | 6 | 10 | 22 | 26 | 64 | 118 | 310 |
|
|
|
|
|
|
|
26 | 79.4 | 3.58 | 112 | 11.6 | 2340 | 35.72 |
其中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作为该昆虫的产卵数
哪一个更适宜作为该昆虫的产卵数![]() 与温度
与温度![]() 的回归方程类型?(给出判断即可,不必说明理由).
的回归方程类型?(给出判断即可,不必说明理由).
(2)根据表中数据,建立![]() 关于
关于![]() 的回归方程;(保留两位有效数字)
的回归方程;(保留两位有效数字)
(3)根据![]() 关于
关于![]() 的回归方程,估计温度为33℃时的产卵数.
的回归方程,估计温度为33℃时的产卵数.
(参考数据:![]() )
)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为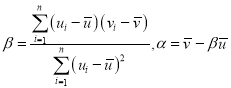 .
.
【答案】(1)![]() 更适宜作为该昆虫的产卵数
更适宜作为该昆虫的产卵数![]() 与温度
与温度![]() 的回归方程类型;(2)
的回归方程类型;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由散点图中点的位置呈现一种指数型的增长,则![]() 更适宜作为该昆虫的产卵数
更适宜作为该昆虫的产卵数![]() 与温度
与温度![]() 的回归方程类型;
的回归方程类型;
(2)将非线性回归方程![]() ,两边取对数得
,两边取对数得![]() ,变成线性回归方程,利用线性回归方程的求法,求解即可;
,变成线性回归方程,利用线性回归方程的求法,求解即可;
(3)将![]() 代入回归方程,即可得出答案.
代入回归方程,即可得出答案.
(1)根据散点图判断,![]() 更适宜作为该昆虫的产卵数
更适宜作为该昆虫的产卵数![]() 与温度
与温度![]() 的回归方程类型.
的回归方程类型.
(2)由![]() ,两边取
,两边取![]() 为底的对数得
为底的对数得![]() .
.
由最小二乘法可得
![]() ,故
,故![]() ,所以
,所以![]()
(3)当![]() 时,
时,![]() .
.

练习册系列答案
相关题目
【题目】对某校高三年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
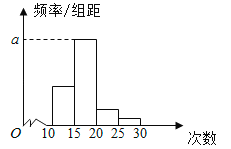
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 15 | 0.30 |
| 29 |
|
|
|
|
| 2 |
|
合计 |
| 1 |
(1)求出表中![]() ,
,![]() 及图中
及图中![]() 的值;
的值;
(2)若该校高三学生人数有500人,试估计该校高三学生参加社区服务的次数在区间![]() 内的人数;
内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间![]() 内的概率.
内的概率.