题目内容
设函数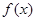 在
在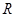 上可导,其导函数
上可导,其导函数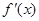 ,且函数
,且函数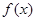 在
在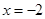 处取得极小值,
处取得极小值,
则函数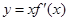 的图象可能是( )
的图象可能是( )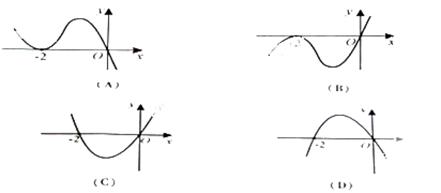
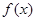 在
在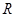 上可导,其导函数
上可导,其导函数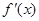 ,且函数
,且函数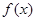 在
在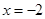 处取得极小值,
处取得极小值,则函数
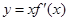 的图象可能是( )
的图象可能是( )
C
解:∵函数f(x)在x=-2处取得极小值,∴f′(-2)=0,
且函数f(x)在x=-2左侧附近为减函数,在x=-2右侧附近为增函数,
即当x<-2时,f′(x)<0,当x>-2时,f′(x)>0,
从而当x<-2时,y=xf′(x)>0,当-2<x<0时,y=xf′(x)<0,
对照选项可知只有C符合题意
故选 C
且函数f(x)在x=-2左侧附近为减函数,在x=-2右侧附近为增函数,
即当x<-2时,f′(x)<0,当x>-2时,f′(x)>0,
从而当x<-2时,y=xf′(x)>0,当-2<x<0时,y=xf′(x)<0,
对照选项可知只有C符合题意
故选 C

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
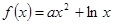 .
.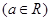
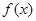 的单调性;
的单调性;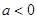 ,若函数
,若函数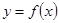 的图象总在直线
的图象总在直线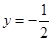 的下方,求
的下方,求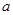 的取值范围;
的取值范围;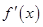 为函数
为函数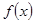 的导函数.若
的导函数.若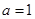 ,试问:在区间
,试问:在区间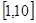 上是否存在
上是否存在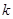 (
(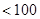 )个正数
)个正数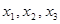 …
…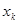 ,使得
,使得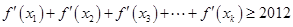 成立?请证明你的结论.
成立?请证明你的结论.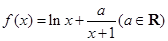 .
.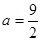 时,求
时,求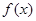 的极值;
的极值;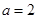 时,试比较
时,试比较 的大小;
的大小;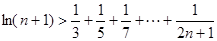 (
(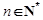 ).
).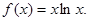
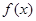 的单调区间和最小值;
的单调区间和最小值;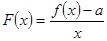 在
在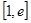 上是最小值为
上是最小值为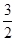 ,求
,求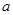 的值;
的值;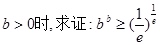 (其中
(其中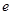 ="2.718" 28…是自然对数的底数).
="2.718" 28…是自然对数的底数).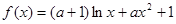 .
.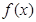 的单调性;
的单调性;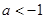 .如果对任意
.如果对任意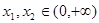 ,
,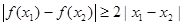 ,求
,求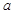 的取值范围.
的取值范围.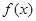 的导函数
的导函数 的大致图象如图所示,则下列结论一定正确的是
的大致图象如图所示,则下列结论一定正确的是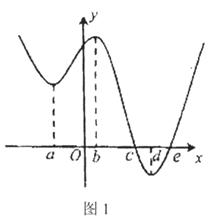
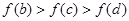
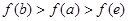
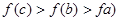
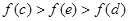
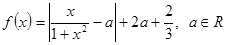
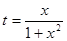 在
在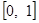 上的单调性;
上的单调性;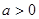 ,求函数
,求函数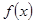 在
在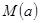 。
。 .
. 是函数
是函数 的极值点,求
的极值点,求 的值;
的值;