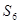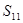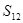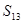题目内容
对于任意的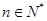 (
(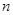 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前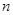 项和等于该数列的前
项和等于该数列的前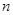 项之积,则称该数列为
项之积,则称该数列为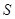 型数列。
型数列。
(1)若数列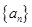 是首项
是首项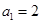 的
的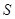 型数列,求
型数列,求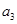 的值;
的值;
(2)证明:任何项数不小于3的递增的正整数列都不是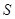 型数列;
型数列;
(3)若数列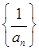 是
是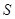 型数列,且
型数列,且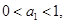 试求
试求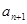 与
与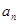 的递推关系,并证明
的递推关系,并证明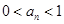 对
对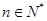 恒成立。
恒成立。
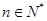 (
(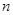 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前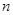 项和等于该数列的前
项和等于该数列的前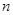 项之积,则称该数列为
项之积,则称该数列为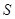 型数列。
型数列。(1)若数列
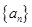 是首项
是首项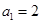 的
的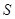 型数列,求
型数列,求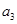 的值;
的值;(2)证明:任何项数不小于3的递增的正整数列都不是
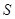 型数列;
型数列;(3)若数列
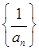 是
是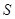 型数列,且
型数列,且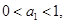 试求
试求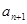 与
与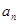 的递推关系,并证明
的递推关系,并证明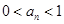 对
对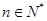 恒成立。
恒成立。(1) (2)证明如下 (3)
(2)证明如下 (3) ,证明如下.
,证明如下.
 (2)证明如下 (3)
(2)证明如下 (3) ,证明如下.
,证明如下.试题分析:(1)新信息题的解答严格按照给的信息作答;(2)构造任意一个递增的正整数数列
 来解决;(3)按照
来解决;(3)按照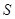 型数列的定义来做.
型数列的定义来做.试题解析:(1)由题意可得
 即
即 所以
所以 又
又 即2+2+
即2+2+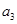 =4
=4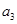 ,所以
,所以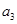 =
=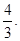
(2)设任意一个递增的正整数数列
 若
若 则由题意可得
则由题意可得 即
即 该等式不成立,所以
该等式不成立,所以 所以
所以 即
即 因为
因为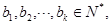 所以
所以 对一切的
对一切的 成立.
成立.因此任何项数不小于3的递增的正整数列都不是
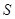 型数列;
型数列;(3)因为数列
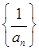 是
是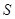 型数列,所以
型数列,所以

 ①.
①. 于是
于是 ②.
②. 两式相减,得
两式相减,得 ③.则
③.则 ④.两式相除,得
④.两式相除,得 整理,得
整理,得 因为
因为 所以
所以 综上所述,
综上所述, 与
与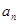 的递推关系为
的递推关系为 因为
因为 所以
所以 当
当 时,
时, 若
若 则
则 所以
所以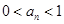 对
对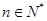 恒成立.
恒成立.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
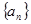 及其前
及其前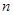 项和
项和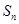 满足:
满足: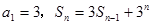 (
(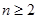 ,
,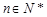 ).
).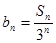 ,
,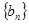 是等差数列;
是等差数列;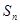 及
及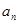 ;
;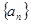 中,
中,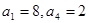 且满足
且满足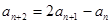 (
( 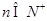 )
)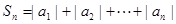 ,求
,求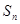 ;
;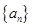 的前三项依次为
的前三项依次为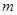 、4、
、4、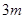 ,前
,前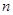 项和为
项和为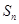 ,且
,且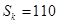 .
.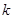 的值;
的值;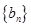 的通项
的通项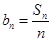 ,证明数列
,证明数列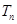 .
.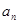 }中,各项都是正数,且a1,
}中,各项都是正数,且a1, 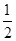 a3,2a2成等差数列,则
a3,2a2成等差数列,则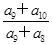 =( )
=( )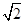
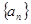 中,
中,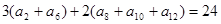 ,则此数列前13项的和为 ( )
,则此数列前13项的和为 ( )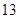
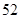
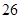
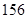
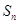 为等差数列
为等差数列 的前
的前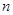 项和,
项和,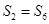 ,
,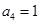 ,正项等比数列
,正项等比数列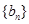 中,
中,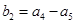 ,
,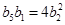 ,则
,则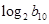 =( )
=( )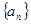 的前
的前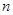 项之和为
项之和为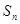 ,若
,若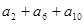 为一个确定的常数,则下列各数中也可以确定的是( )
为一个确定的常数,则下列各数中也可以确定的是( )