题目内容
已知数列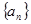 及其前
及其前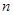 项和
项和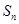 满足:
满足: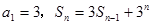 (
(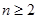 ,
,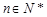 ).
).
(1)证明:设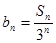 ,
,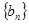 是等差数列;
是等差数列;
(2)求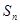 及
及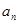 ;
;
(3)判断数列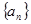 是否存在最大或最小项,若有则求出来,若没有请说明理由.
是否存在最大或最小项,若有则求出来,若没有请说明理由.
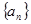 及其前
及其前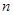 项和
项和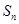 满足:
满足: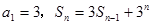 (
(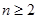 ,
,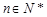 ).
).(1)证明:设
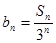 ,
,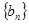 是等差数列;
是等差数列;(2)求
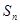 及
及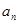 ;
;(3)判断数列
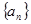 是否存在最大或最小项,若有则求出来,若没有请说明理由.
是否存在最大或最小项,若有则求出来,若没有请说明理由.(1)见解析;(2)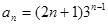 ,
,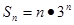 ;(3)数列
;(3)数列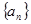 有最小项,无最大项,最小项为
有最小项,无最大项,最小项为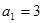
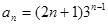 ,
,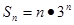 ;(3)数列
;(3)数列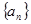 有最小项,无最大项,最小项为
有最小项,无最大项,最小项为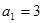
试题分析:(1)直接求出
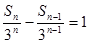 ,从而证明
,从而证明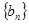 是等差数列;(2)先由(1)可得
是等差数列;(2)先由(1)可得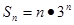 ,然后由
,然后由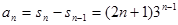 ,注意检验当
,注意检验当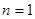 时是否适用 .(3)先判定数列是递增数列,从而确定只有最小项无最大项,最小项为
时是否适用 .(3)先判定数列是递增数列,从而确定只有最小项无最大项,最小项为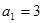 ,注意运用函数的思想方法解决数列问题.
,注意运用函数的思想方法解决数列问题.试题解析:(1)
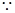
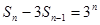 ∴
∴ 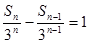 (
(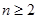 ) 2分
) 2分设
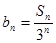 则
则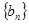 是公差为1的等差数列 3分
是公差为1的等差数列 3分(2) 又
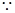
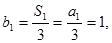 ∴
∴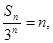 ∴
∴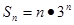 5分
5分当
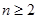 时,
时, 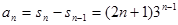 7分
7分又
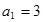 满足上式 8分
满足上式 8分∴
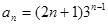
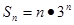 9分
9分(3)
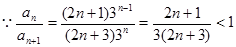 11分
11分又
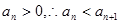 ,则数列
,则数列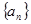 为递增数列 12分
为递增数列 12分∴数列
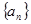 有最小项,无最大项,此时最小项为
有最小项,无最大项,此时最小项为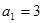 13分
13分 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
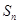 为数列
为数列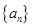 的前
的前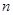 项和,对任意的
项和,对任意的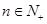 ,都有
,都有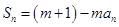 (
(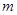 为正常数).
为正常数).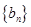 满足
满足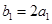 ,
,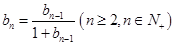 ,求数列
,求数列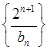 的前
的前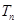 .
.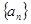 的前
的前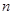 项和为
项和为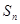 ,已知
,已知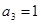 ,
,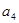 是
是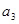 和
和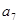 的等比中项.
的等比中项.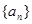 是首项是2,公比为q的等比数列,其中
是首项是2,公比为q的等比数列,其中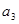 是
是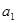 与
与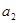 的等差中项.
的等差中项. 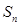
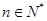 (
(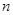 不超过数列的项数),若数列的前
不超过数列的项数),若数列的前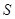 型数列。
型数列。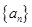 是首项
是首项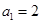 的
的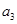 的值;
的值;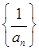 是
是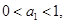 试求
试求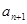 与
与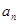 的递推关系,并证明
的递推关系,并证明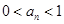 对
对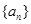 的前13项之和为
的前13项之和为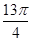 ,则
,则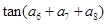 等于( )
等于( )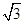
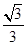
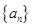 的首项及公差均是正整数,前
的首项及公差均是正整数,前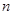 项和为
项和为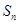 ,且
,且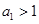 ,
,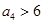 ,
,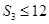 ,则
,则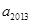 =
= 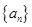 、
、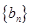 都是等差数列,若
都是等差数列,若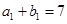 ,
,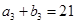 ,则
,则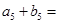 .
.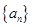
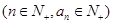 ,若
,若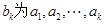 中最大值
中最大值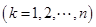 ,则称数列
,则称数列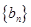 为数列
为数列