题目内容
设抛物线y2=4x截直线y=2x+k所得弦长|AB|=3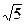 .
.
(1)求k的值;
(2)以弦AB为底边,x轴上的P点为顶点组成的三角形面积为39时,求点P的坐标.
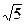 .
.(1)求k的值;
(2)以弦AB为底边,x轴上的P点为顶点组成的三角形面积为39时,求点P的坐标.
P点为(15,0)或(-11,0).
(1)设A(x1,y1)、B(x2,y2),
由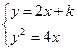 得4x2+4(k-1)x+k2=0,Δ=16(k-1)2-16k2>0.
得4x2+4(k-1)x+k2=0,Δ=16(k-1)2-16k2>0.
∴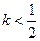 .
.
又由韦达定理有x1+x2=1-k,x1x2=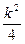 ,
,
∴|AB|=
= ,
,
即 .
.
∴k=-4.
(2)设x轴上点P(x,0),P到AB的距离为d,则
 ,
,
S△PBC=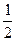 ·
·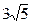 ·
·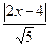 =39,
=39,
∴|2x-4|=26.
∴x=15或x=-11.
∴P点为(15,0)或(-11,0).
由
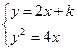 得4x2+4(k-1)x+k2=0,Δ=16(k-1)2-16k2>0.
得4x2+4(k-1)x+k2=0,Δ=16(k-1)2-16k2>0.∴
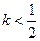 .
.又由韦达定理有x1+x2=1-k,x1x2=
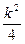 ,
,∴|AB|=

=
 ,
,即
 .
.∴k=-4.
(2)设x轴上点P(x,0),P到AB的距离为d,则
 ,
,S△PBC=
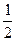 ·
·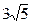 ·
·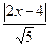 =39,
=39,∴|2x-4|=26.
∴x=15或x=-11.
∴P点为(15,0)或(-11,0).

练习册系列答案
相关题目
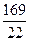 x
x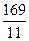 x
x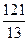 y
y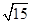 ,求抛物线的标准方程.
,求抛物线的标准方程.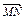 =2
=2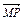 ,
,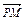 ⊥
⊥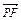 ,当点P
,当点P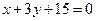 上抛物线的标准方程.
上抛物线的标准方程.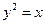 ,如图所示表示平行于对称轴
,如图所示表示平行于对称轴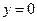 (即
(即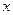 轴)的光线在抛物线上的点
轴)的光线在抛物线上的点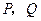 的反射情况,设
的反射情况,设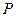 纵坐标为
纵坐标为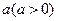 ,
,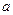 取何值时,从入射点
取何值时,从入射点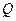 的光线路程
的光线路程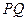 最短.
最短.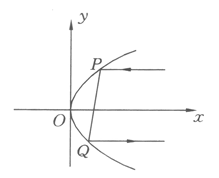
 相交于B、C两点,点
相交于B、C两点,点
 轴上的射影分别为
轴上的射影分别为 , P是线段BC上的点,且适合
, P是线段BC上的点,且适合 ,求
,求 的重心Q的轨迹方程,并说明该轨迹是什么图形.
的重心Q的轨迹方程,并说明该轨迹是什么图形.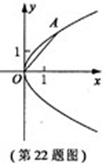
 中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在
中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在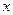 轴上。
轴上。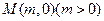 的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为
的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为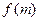 ,求
,求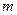 的表达式。
的表达式。