题目内容
已知双曲线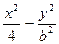 ="1"
="1" 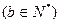 的两个焦点为
的两个焦点为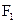 、
、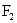 ,P是双曲线上的一点,
,P是双曲线上的一点,
且满足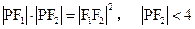 ,
,
(1)求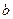 的值;
的值;
(2)抛物线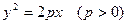 的焦点F与该双曲线的右顶点重合,斜率为1的直线经过点F与该抛物线交于A、B两点,求弦长|AB|.
的焦点F与该双曲线的右顶点重合,斜率为1的直线经过点F与该抛物线交于A、B两点,求弦长|AB|.
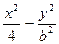 ="1"
="1" 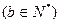 的两个焦点为
的两个焦点为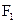 、
、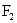 ,P是双曲线上的一点,
,P是双曲线上的一点,且满足
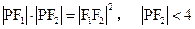 ,
,(1)求
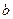 的值;
的值;(2)抛物线
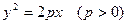 的焦点F与该双曲线的右顶点重合,斜率为1的直线经过点F与该抛物线交于A、B两点,求弦长|AB|.
的焦点F与该双曲线的右顶点重合,斜率为1的直线经过点F与该抛物线交于A、B两点,求弦长|AB|.(1) 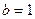 (2)16
(2)16
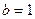 (2)16
(2)16(1)根据题意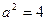 ,
,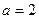
又,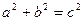 ,
,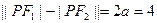 ,又|P F
,又|P F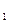 |•|PF
|•|PF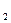 |="|" F
|="|" F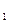 F
F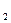 |
|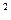 =
=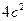 , |P F
, |P F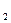 |<4, 得
|<4, 得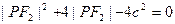 在区间(0,4)上有解, 所以
在区间(0,4)上有解, 所以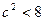
因此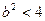 ,又
,又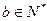 ,所以
,所以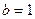
(2)双曲线方程为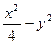 =1,右顶点坐标为(2,0),即
=1,右顶点坐标为(2,0),即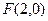
所以抛物线方程为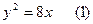 直线方程为
直线方程为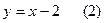
由(1)(2)两式联立,解得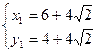 和
和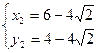
所以弦长|AB|=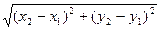 =16
=16
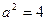 ,
,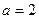
又,
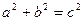 ,
,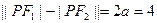 ,又|P F
,又|P F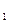 |•|PF
|•|PF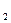 |="|" F
|="|" F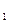 F
F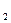 |
|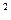 =
=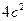 , |P F
, |P F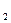 |<4, 得
|<4, 得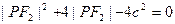 在区间(0,4)上有解, 所以
在区间(0,4)上有解, 所以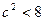
因此
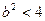 ,又
,又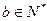 ,所以
,所以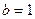
(2)双曲线方程为
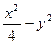 =1,右顶点坐标为(2,0),即
=1,右顶点坐标为(2,0),即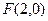
所以抛物线方程为
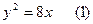 直线方程为
直线方程为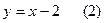
由(1)(2)两式联立,解得
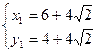 和
和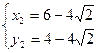
所以弦长|AB|=
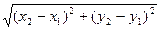 =16
=16
练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
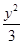 =1的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则
=1的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则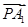 ·
·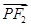 的最小值为________.
的最小值为________.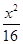 -
-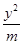 =1的离心率为
=1的离心率为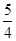 ,则m等于________.
,则m等于________.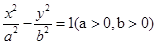 的左、右焦点分别是
的左、右焦点分别是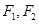 ,过
,过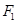 作倾斜角为
作倾斜角为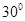 的直线交双曲线右支于点M,若
的直线交双曲线右支于点M,若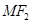 垂直于x轴,则双曲线的离心率为( )
垂直于x轴,则双曲线的离心率为( )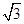
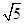
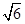
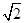
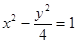 的渐近线方程是( )
的渐近线方程是( )



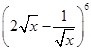 的展开式中含
的展开式中含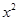 项的系数是
项的系数是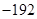 ;
;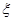 服从正态分布N(2,
服从正态分布N(2,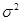 )(
)(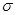 >0).若
>0).若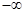 ,1)内取值的概率为0.15,则
,1)内取值的概率为0.15,则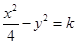 的渐近线方程为
的渐近线方程为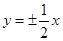 ,则k=1.其中正确命题的序号是 .
,则k=1.其中正确命题的序号是 .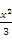 -
- 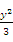 =1相交于A,B两点,若△ABF为等边三角形,则p=___________.
=1相交于A,B两点,若△ABF为等边三角形,则p=___________.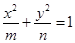
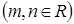 的右焦点与抛物线
的右焦点与抛物线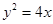 的焦点重合,
的焦点重合,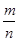 ="____________" .
="____________" .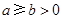 时,双曲线
时,双曲线 的离心率
的离心率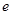 的取值范围是( )
的取值范围是( )