题目内容
如图,若射线 上分别存在点
上分别存在点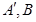 与
与 ,则三角形面积之比
,则三角形面积之比  ,如图若不在同一平面内的射线
,如图若不在同一平面内的射线 和
和 上分别存在点
上分别存在点 点
点 和点
和点 ,则三棱锥体积之比
,则三棱锥体积之比 

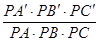
解析试题分析:由平面图形中点的性质类比推理出空间里的线的性质,由平面图形中线的性质类比推理出空间中面的性质,由平面图形中面的性质类比推理出空间中体的性质.根据已知中射线 上分别存在点
上分别存在点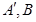 与
与 ,则三角形面积之比
,则三角形面积之比  ,那么可知体积的比就是面积比乘以高的比得到 ,那么结合类比推理可知
,那么可知体积的比就是面积比乘以高的比得到 ,那么结合类比推理可知
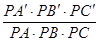 ,故答案为
,故答案为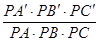 。
。
考点:类比推理
点评:本试题考查了类比推理,一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想)

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
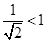 ;②
;②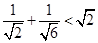 ;③
;③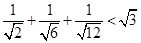 ;…
;…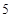 个不等式为 .
个不等式为 . 的三边长为
的三边长为 ,内切圆半径为
,内切圆半径为 (用
(用 ),则
),则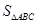
 ;类比这一结论有:若三棱锥
;类比这一结论有:若三棱锥 的内切球半径为
的内切球半径为 ,则三棱锥体积
,则三棱锥体积

 ,AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论:
,AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论: ,给出空间中三棱锥的有关结论:________
,给出空间中三棱锥的有关结论:________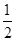 r(a+b+c),根据类比思想,若四面体的内切球半径为R,四个面的面积分别为S1、S2、S3、S4,则此四面体的体积V=________.
r(a+b+c),根据类比思想,若四面体的内切球半径为R,四个面的面积分别为S1、S2、S3、S4,则此四面体的体积V=________. 当
当 时,观察下列等式:
时,观察下列等式:  ,
,  ,
, ,
, ,
, ,
,
 .
.  个等式为
个等式为 ,
, ,
, ,
, ,
, ,可以得出的一般结论是
,可以得出的一般结论是