题目内容
在平面几何里,已知直角三角形ABC中,角C为
 ,AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论:
,AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论:
有三角形的勾股定理,给出空间中三棱锥的有关结论:________
若三角形ABC的外接圆的半径为 ,给出空间中三棱锥的有关结论:________
,给出空间中三棱锥的有关结论:________
在三棱锥O-ABC中,若三个侧面两两垂直,则 ;在三棱锥O-ABC中,若三个侧面两两垂直,且三条侧棱长分别为a,b,c,则其外接球的半径为
;在三棱锥O-ABC中,若三个侧面两两垂直,且三条侧棱长分别为a,b,c,则其外接球的半径为
解析试题分析:平面几何图形边长满足长度关系式,类比立体几何图形面积满足一定关系式,三角形中同一点出发的两线垂直,类比立体几何中同一条棱出发的三面互相垂直,直角三角形三边的平方关系类比立体几何中的三面平方关系得关系式
直角三角形外接圆半径与两直角边有关系式,类比立体几何棱锥外接球半径与互相垂直的三条棱有关系式
考点:知识的类比迁移能力
点评:比较已知中给定的条件与所要类比的问题,找到他们之间的类似点,采用已知中的关系式形式类比写出所求的关系式

练习册系列答案
相关题目
 的首项是
的首项是 ,随后两项都是
,随后两项都是 ,接下来
,接下来 项都是
项都是 项都是
项都是 ,若
,若 ,
, ,则
,则 .
. ,
,  ,
,  , ……
, ……
 个等式:
个等式: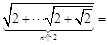 .
. ,
, ,
, ,……则可以猜想
,……则可以猜想 
 分别与实数
分别与实数 对应,则线段
对应,则线段 的中点
的中点 与实数
与实数 对应,由此结论类比到平面得,若平面上不共线的三点
对应,由此结论类比到平面得,若平面上不共线的三点 分别与二元实数对
分别与二元实数对 对应,则
对应,则 的重心
的重心 与 对应.
与 对应. 上分别存在点
上分别存在点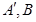 与
与 ,则三角形面积之比
,则三角形面积之比  ,如图若不在同一平面内的射线
,如图若不在同一平面内的射线 和
和 上分别存在点
上分别存在点 点
点 和点
和点

 ,
, 则
则 边上的高
边上的高 ; 拓展到空间,如图,三棱锥
; 拓展到空间,如图,三棱锥 的三条侧棱SB、SB、SC两两相互垂直,且
的三条侧棱SB、SB、SC两两相互垂直,且 ,则点
,则点 到面
到面 的距离
的距离

 的取值范围是 .
的取值范围是 .
 表示第
表示第 幅图的蜂巢总数.则
幅图的蜂巢总数.则 =_____;
=_____;