题目内容
若三角形的内切圆半径为r,三边的长分别为a,b,c,则三角形的面积S=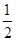 r(a+b+c),根据类比思想,若四面体的内切球半径为R,四个面的面积分别为S1、S2、S3、S4,则此四面体的体积V=________.
r(a+b+c),根据类比思想,若四面体的内切球半径为R,四个面的面积分别为S1、S2、S3、S4,则此四面体的体积V=________.
V=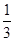 R(S1+S2+S3+S4)
R(S1+S2+S3+S4)
解析试题分析:因为三角形的内切圆半径为r,三边的长分别为a,b,c,则三角形的面积S=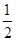 r(a+b+c),所以根据类比思想,此四面体的体积是V=
r(a+b+c),所以根据类比思想,此四面体的体积是V=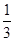 R(S1+S2+S3+S4)。
R(S1+S2+S3+S4)。
考点:本题主要考查类比推理。
点评:类比推理是根据两个或两类对象有部分属性相同,从而推出它们的其他属性也相同的推理。

练习册系列答案
相关题目
 ”时,某同学学到了如下一种方法:先改写第k项:
”时,某同学学到了如下一种方法:先改写第k项: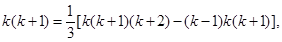 由此得
由此得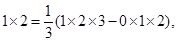
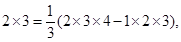
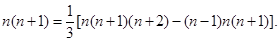
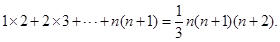
 ”,
”,
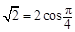 ,
, 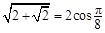 ,
, 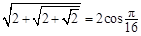 , ……
, ……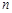
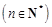 个等式:
个等式: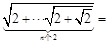 .
.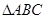 的两边AB、AC互相垂直,则
的两边AB、AC互相垂直,则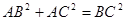 。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。
。”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面积与底面积间的关系,可以得到的正确结论是:“设三棱锥A-BCD的三个侧面ABC 、ACD、ADB两两互相垂直,则 ”。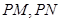 上分别存在点
上分别存在点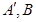 与
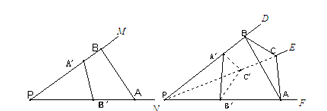
与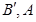 ,则三角形面积之比
,则三角形面积之比 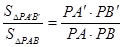 ,如图若不在同一平面内的射线
,如图若不在同一平面内的射线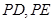 和
和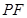 上分别存在点
上分别存在点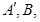 点
点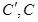 和点
和点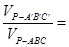
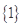 ,第二组含两个数
,第二组含两个数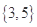 ,第三组含三个数
,第三组含三个数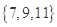 ,第四组含四个数
,第四组含四个数 ,…,现观察猜想每组内各数之和为
,…,现观察猜想每组内各数之和为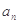 与其组的编号数
与其组的编号数 的关系为 .
的关系为 .
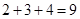
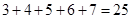
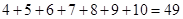
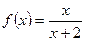 ,
,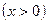 观察
观察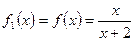
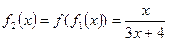

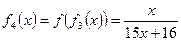 ……
……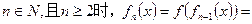
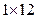 ,
,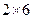 ,
,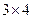 三种,其中
三种,其中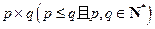 是正整数
是正整数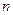 的最佳分解时,我们规定函数
的最佳分解时,我们规定函数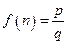 ,例如
,例如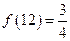 .关于函数
.关于函数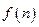 有下列叙述:①
有下列叙述:①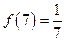 ,②
,②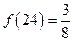 ,③
,③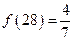 ,④
,④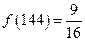 .其中正确的序号为 (填入所有正确的序号).
.其中正确的序号为 (填入所有正确的序号).