题目内容
已知函数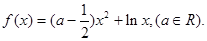
(Ⅰ)当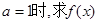 在区间
在区间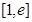 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)若在区间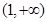 上,函数
上,函数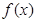 的图象恒在直线
的图象恒在直线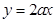 下方,求
下方,求 的取值范围.
的取值范围.
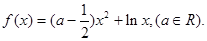
(Ⅰ)当
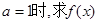 在区间
在区间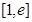 上的最大值和最小值;
上的最大值和最小值;(Ⅱ)若在区间
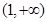 上,函数
上,函数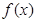 的图象恒在直线
的图象恒在直线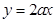 下方,求
下方,求 的取值范围.
的取值范围.(Ⅰ) ,
,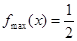 (Ⅱ)
(Ⅱ)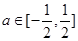
 ,
,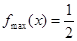 (Ⅱ)
(Ⅱ)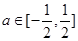
(Ⅰ)当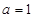 时,
时, ∴
∴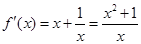 (2’)对于
(2’)对于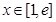 ,有
,有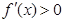 ,∴
,∴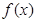 在区间
在区间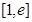 上为增函数。∴
上为增函数。∴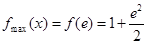 ,
,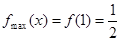 (5’)
(5’)
(Ⅱ)令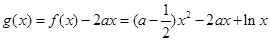 ,则
,则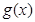 的定义域为
的定义域为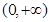 。(6’)
。(6’)
在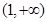 区间上,函数
区间上,函数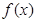 的图象恒在直线
的图象恒在直线 下方等价于
下方等价于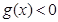 在区间
在区间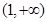 上恒成立。
上恒成立。
∵ =
=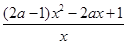 =
=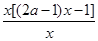 (8’)
(8’)
①若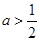 ,令
,令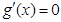 ,解得
,解得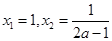 。当
。当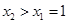 ,即
,即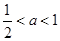 时,在
时,在 上有
上有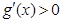 ,
,
此时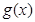 在区间
在区间 上是增函数,并且在该区间上有
上是增函数,并且在该区间上有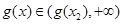 ,不合题意;
,不合题意;
当 ,即
,即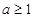 ,同理可知,
,同理可知,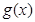 在区间
在区间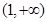 上,有
上,有 ,也不合题意;(10’)
,也不合题意;(10’)
②若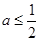 时,则有
时,则有 ,此时在区间
,此时在区间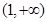 上恒有
上恒有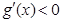 ,从而
,从而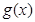 在区间
在区间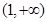 上是减函数;
上是减函数;
要使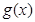 <0,在此区间上恒成立,只须满足
<0,在此区间上恒成立,只须满足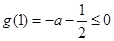
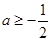 ,由此求得
,由此求得 的范围是
的范围是 。(12’)
。(12’)
综合①②可知,当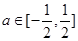 时,函数
时,函数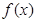 的图象恒在直线
的图象恒在直线 下方。
下方。
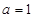 时,
时, ∴
∴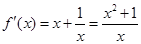 (2’)对于
(2’)对于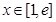 ,有
,有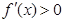 ,∴
,∴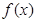 在区间
在区间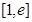 上为增函数。∴
上为增函数。∴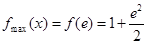 ,
,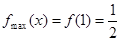 (5’)
(5’)(Ⅱ)令
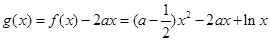 ,则
,则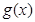 的定义域为
的定义域为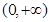 。(6’)
。(6’)在
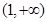 区间上,函数
区间上,函数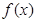 的图象恒在直线
的图象恒在直线 下方等价于
下方等价于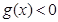 在区间
在区间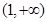 上恒成立。
上恒成立。∵
 =
=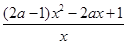 =
=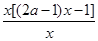 (8’)
(8’)①若
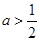 ,令
,令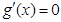 ,解得
,解得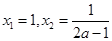 。当
。当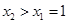 ,即
,即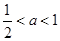 时,在
时,在 上有
上有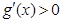 ,
,此时
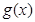 在区间
在区间 上是增函数,并且在该区间上有
上是增函数,并且在该区间上有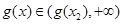 ,不合题意;
,不合题意;当
 ,即
,即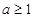 ,同理可知,
,同理可知,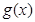 在区间
在区间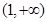 上,有
上,有 ,也不合题意;(10’)
,也不合题意;(10’)②若
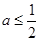 时,则有
时,则有 ,此时在区间
,此时在区间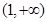 上恒有
上恒有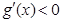 ,从而
,从而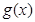 在区间
在区间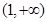 上是减函数;
上是减函数;要使
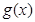 <0,在此区间上恒成立,只须满足
<0,在此区间上恒成立,只须满足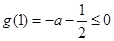
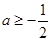 ,由此求得
,由此求得 的范围是
的范围是 。(12’)
。(12’)综合①②可知,当
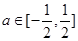 时,函数
时,函数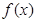 的图象恒在直线
的图象恒在直线 下方。
下方。
练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
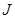 型卡车将某种水果运送(满载)到相距400km的水果批发市场.据测算,
型卡车将某种水果运送(满载)到相距400km的水果批发市场.据测算, (单位:
(单位: )与速度
)与速度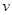 (单位:km/h)的关系近似地满足
(单位:km/h)的关系近似地满足 ,除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为7.5元/L.
,除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为7.5元/L.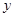 (元)(不计返程费用),将
(元)(不计返程费用),将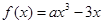 .
.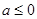 时,求函数
时,求函数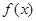 单调区间;
单调区间;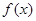 在区间[1,2]上的最小值为
在区间[1,2]上的最小值为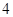 ,求
,求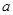 的值.
的值.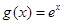 ,
,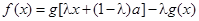 ,其中
,其中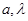 是常数,且
是常数,且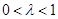 .
.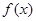 的极值;
的极值;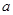 ,存在正数
,存在正数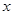 ,使不等式
,使不等式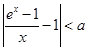 成立;
成立;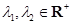 ,且
,且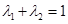 ,证明:对任意正数
,证明:对任意正数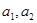 都有:
都有: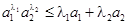 .
. 与
与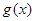 是定义在
是定义在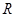 上的两个可导函数,若
上的两个可导函数,若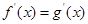 ,则
,则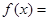
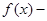
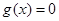
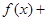
 的图象与
的图象与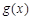 的图象关于直线
的图象关于直线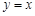 对称。
对称。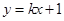 与
与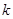 的值;
的值;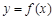 与曲线
与曲线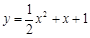 公共点的个数.
公共点的个数.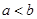 ,比较
,比较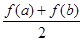 与
与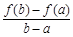 的大小, 并说明理由.
的大小, 并说明理由. 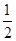 x2,则f′(1)=____.
x2,则f′(1)=____.